题目内容
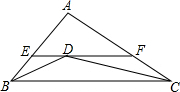 如图,在△ABC中,已知∠B和∠C的平分线相交于点D,过点D作EF∥BC交AB、AC于点E、F,若△AEF的周长为9,BC=6,则△ABC的周长为( )
如图,在△ABC中,已知∠B和∠C的平分线相交于点D,过点D作EF∥BC交AB、AC于点E、F,若△AEF的周长为9,BC=6,则△ABC的周长为( )| A、18 | B、17 | C、16 | D、15 |
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:根据角平分线的定义可得∠DBC=∠DBE,再根据两直线平行,内错角相等可得∠DBC=∠BDE,然后求出∠DBE=∠BDE,根据等角对等边可得BE=DE,同理得到CF=DF,从而求出△AEF的周长=AB+AC,再根据三角形的周长的定义解答即可.
解答:解:∵BD平分∠ABC,
∴∠DBC=∠DBE,
∵EF∥BC,
∴∠DBC=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE,
同理可得,CF=DF,
∴△AEF的周长=AE+DE+DF+AF=AE+BE+AF+CF=AB+AC=9,
∵BC=6,
∴△ABC的周长=9+6=15.
故选D.
∴∠DBC=∠DBE,
∵EF∥BC,
∴∠DBC=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE,
同理可得,CF=DF,
∴△AEF的周长=AE+DE+DF+AF=AE+BE+AF+CF=AB+AC=9,
∵BC=6,
∴△ABC的周长=9+6=15.
故选D.
点评:本题考查了等腰三角形的判定与性质,平行线的性质,熟记性质并准确识图求出△AEF的周长=AB+AC是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
比较a与3a的大小,正确的是( )
| A、3a>a | B、3a=a |
| C、3a<a | D、上述情况都可能 |
下列方程有两个不相等的实数根的是( )
| A、x2+2=0 |
| B、x2-2x=-1 |
| C、x2+2x+5=0 |
| D、x2-3x+1=0 |
抛物线y=-x2+1的对称轴是( )
| A、直线x=1 |
| B、直线x=0 |
| C、直线x=-1 |
| D、直线y=0 |
已知直线y=2x与直线y=kx+5互相平行,则k的值为( )
| A、k=-2 | B、k=2 |
| C、k=±2 | D、无法确定k的值 |
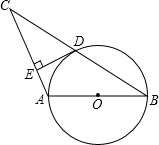 已知:如图,AB为⊙O的直径,⊙O过BC的中点D,且DE⊥AC,
已知:如图,AB为⊙O的直径,⊙O过BC的中点D,且DE⊥AC,