题目内容
 如图所示,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,那么△BED面积是
如图所示,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,那么△BED面积是分析:S△BED=
DE•AB,所以需求DE的长.根据∠C′BD=∠DBC=∠BDA得DE=BE,设DE=x,则AE=8-x.根据勾股定理求BE即DE的长.
| 1 |
| 2 |
解答:解:∵AD∥BC,
∴∠DBC=∠BDA.
∵∠C′BD=∠DBC,
∴∠C′BD=∠BDA.
∴DE=BE.
设DE=x,则AE=8-x.在△ABE中,
x2=42+(8-x)2.
解得x=5.
∴S△DBE=
×5×4=10(平方单位).
∴∠DBC=∠BDA.
∵∠C′BD=∠DBC,
∴∠C′BD=∠BDA.
∴DE=BE.
设DE=x,则AE=8-x.在△ABE中,
x2=42+(8-x)2.
解得x=5.
∴S△DBE=
| 1 |
| 2 |
点评:此题通过折叠变换考查了三角形的有关知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后对应边、角相等.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
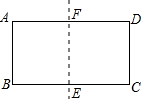 如图所示,将矩形ABCD沿两条较长边的中点的连线对折,如果矩形BEFA与矩形ABCD相似,那么AB:AD等于( )
如图所示,将矩形ABCD沿两条较长边的中点的连线对折,如果矩形BEFA与矩形ABCD相似,那么AB:AD等于( )A、
| ||
B、1:
| ||
C、
| ||
D、1:
|

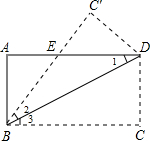 如图所示,将矩形ABCD沿着直线BD折叠,使点C落在点C′,BC′交AD于点E,AD=8,AB=4.
如图所示,将矩形ABCD沿着直线BD折叠,使点C落在点C′,BC′交AD于点E,AD=8,AB=4.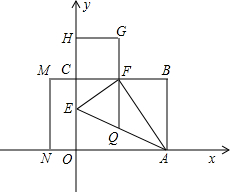 理由.
理由.