题目内容

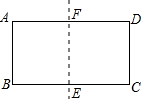精英家教网如图所示，将矩形ABCD沿两条较长边的中点的连线对折，如果矩形BEFA与矩形ABCD相似，那么AB：AD等于（　　）
A、
2
：1
B、1：
2
C、
3
：1
D、1：
3
分析：矩形ABCD对折后所得矩形与原矩形相似，则矩形ABCD∽矩形BEFA，设矩形的长边长是a，短边长是b．则AB=CD=b，AD=BC=a，BE=AF=
a
2
，根据相似多边形的性质即可得．
解答：解：根据矩形相似，对应边的比相等得到：
AB
AD
=
BE
AB
，
即：
b
a
=
a
2
b
，
则b2=
a2
2
，
∴
a2
b2
=2，
∴
a
b
=
2
：1，
则AB：AD=1：
2
．
故选B．
点评：本题运用了两个矩形相似，对应边的比相等这一性质，分清对应边是解决本题的关键．
练习册系列答案
相关题目
8、如图所示，将矩形纸片先沿虚线AB按箭头方向向右对折，接着对折后的纸片沿虚线CD向下对折，然后剪下一个小三角形，再将纸片打开，则打开后的展开图是（　　）
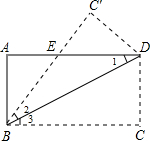精英家教网如图所示，将矩形ABCD沿着直线BD折叠，使点C落在点C′，BC′交AD于点E，AD=8，AB=4．
（1）求证：△BED是等腰三角形；
（2）求△BED的面积．
如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM=|CE-EO|，再以CM、CO为边作矩形CMNO．
（1）试比较EO、EC的大小，并说明理由；
（2）令m=
S四边形CFGH
S四边形CMNO
，请问m是否为定值？若是，请求出m的值；若不是，请说明理由；
（3）在（2）的条件下，若CO=1，CE=
1
3
，Q为AE上一点且QF=
2
3
，抛物线y=mx2+bx+c经过C、Q两点，请求出此抛物线的解析式；
（4）在（3）的条件下，若抛物线y=mx2+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，使得以P、B、K为顶点的三角形与△AEF相似？若存在，请求直线KP与y轴的交点T的坐标；若不存在，请说明精英家教网理由．
精英家教网如图所示，将矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于E，AD=8，AB=4，那么△BED面积是
 
平方单位．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网