Question

【题目】如图，在中，，以为直径作交于点.过点作，垂足为，且交的延长线于点.

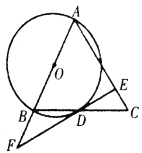
（1）求证：是的切线；

（2）若，，求的长.

Answer 1

【答案】（1）见解析；（2）BD长为5．

【解析】

（1）连接OD，AD，根据等腰三角形三线合一得BD=CD，根据三角形的中位线可得OD∥AC，所以得OD⊥EF，从而得结论；
（2）根据等腰三角形三线合一的性质证得∠BAD=∠BAC=30°，由30°的直角三角形的性质即可求得BD．

（1）证明：连接OD，AD，

∵AB是⊙O的直径，

∴∠ADB=90°，

∴AD⊥BC，

∵AB＝AC，

∴BD＝CD，

∵OA＝OB，

∴OD是△BAC的中位线，

∴OD∥AC，

∵EF⊥AC，

∴OD⊥EF，

∴EF是⊙O的切线；

（2）解：∵AB＝AC，AD⊥BC，

∴∠BAD＝∠BAC＝30°，

∴BD＝AB＝×10＝5,

即BD 长为5．