题目内容
12.三位同学对下面这个问题提出了自己的看法:若关于x,y的方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,方程组$\left\{\begin{array}{l}{3{a}_{1}x+2{b}_{1}y=5{c}_{1}}\\{3{a}_{2}+2{b}_{2}y=5{c}_{2}}\end{array}\right.$的解.
甲说:“这个题目好象条件不够,不能求解”;
乙说:“它们的系数有一定的规律,可以试试”;
丙说:“能不能把第二个方程组的两个方程的两边都除以5,将方程组化为$\left\{\begin{array}{l}{{a}_{1}(\frac{3x}{5})+{b}_{1}(\frac{2y}{5})={c}_{1}}\\{{a}_{2}(\frac{3x}{5})+{b}_{2}(\frac{2y}{5})={c}_{2}}\end{array}\right.$,然后通过换元替代的方法来解决?”
你认为这个方程组有解吗?如果认为有,求出它的解.
分析 方程组有解,理由为:根据已知方程组的解,将所求方程组变形后仿照解的规律求出x与y的值即可.
解答 解:方程组有解,
∵方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,
∴方程组$\left\{\begin{array}{l}{{a}_{1}(\frac{3x}{5})+{b}_{1}(\frac{2y}{5})={c}_{1}}\\{{a}_{2}(\frac{3x}{5})+{b}_{2}(\frac{2y}{5})={c}_{2}}\end{array}\right.$解为$\left\{\begin{array}{l}{\frac{3x}{5}=3}\\{\frac{2y}{5}=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=5}\\{y=10}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.
(1)填表:
(2)要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品实际售价应定为多少元?
(1)填表:
| 每月的销售量(件) | 每件商品销售利润(元) | |
| 降价前 | 60 | 80 |
| 降价后 | 60+5x | 80-x |
2.在?ABCD中,∠A:∠B:∠C:∠D可能是( )
| A. | 1:2:3:4 | B. | 2:3:2:3 | C. | 2:2:1:1 | D. | 2:3:3:2 |
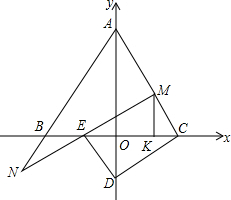 已知B(-2,0),C(2,0),点A是y轴正半轴上一点,CD⊥AC交y轴于D,M为AC上一动点.N为AB延长线一动点,且满足AM+AN=2AC,MN交BC于E,连DE.
已知B(-2,0),C(2,0),点A是y轴正半轴上一点,CD⊥AC交y轴于D,M为AC上一动点.N为AB延长线一动点,且满足AM+AN=2AC,MN交BC于E,连DE. 如图所示,在?ABCD中,∠BAD的平分线与∠ABC的平分线、∠ADC的平分线分别交于点E和点F,∠BCD的平分线与∠ABC的平分线、∠ADC的平分线分别交于点H和点G.
如图所示,在?ABCD中,∠BAD的平分线与∠ABC的平分线、∠ADC的平分线分别交于点E和点F,∠BCD的平分线与∠ABC的平分线、∠ADC的平分线分别交于点H和点G.