题目内容
已知y=-2x+3的图象与y=x2的图象交于A、B两点,O为坐标原点,则△AOB的面积= .
考点:二次函数的性质
专题:
分析:联立两解析式可求得两点的坐标为A(1,1)、B(-3,9),过A作AC⊥x轴,过B作BD⊥x轴,分别交x轴于点C、D两点,则可求得AC=1,CO=1,BD=9,OD=3,再利用面积和差可求得△AOB的面积.
解答: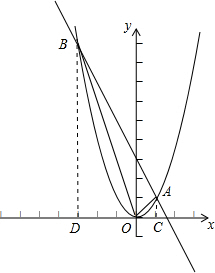 解:
解:
联立两函数解析式得
,解得
或
,
∴A(1,1),B(-3,9),
如图,过A作AC⊥x轴,过B作BD⊥x轴,分别交x轴于点C、D两点,
则可求得AC=1,CO=1,BD=9,OD=3,
∴DC=3+1=4,
∴S梯形ABDC=
(AC+BD)•CD=
×(1+9)×4=20,S△BOD=
OD•BD=
×3×9=13.5,S△AOC=
OC•AC=
×1×1=0.5,
∴S△AOB=S梯形ABDC-S△BOD-S△AOC=20-13.5-0.5=6,
故答案为:6.
 解:
解:联立两函数解析式得
|
|
|
∴A(1,1),B(-3,9),
如图,过A作AC⊥x轴,过B作BD⊥x轴,分别交x轴于点C、D两点,
则可求得AC=1,CO=1,BD=9,OD=3,
∴DC=3+1=4,
∴S梯形ABDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOB=S梯形ABDC-S△BOD-S△AOC=20-13.5-0.5=6,
故答案为:6.
点评:本题主要考查图象交点的求法,利用方程组求得交点坐标并把所求三角形的面积转化成梯形的面积减去两个三角形的面积是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
二月份的月历,竖着取连续的三个数字,它们的和可能是( )
| A、35 | B、18 | C、72 | D、33 |
下列各式,分解因式正确的是( )
| A、a2-b2=(a-b)2 | ||
| B、a2-2ab+b2=(a-b)2 | ||
C、x2+x3=x3(
| ||
| D、xy+xz+x=x(y+z) |
在下面图形中,不能折成正方体的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.
如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.