题目内容
在Rt△ABC中,∠C=90°,BC=6,AC=8,点D在线段AC上从C向A运动.若设CD=x,△ABD的面积为y.
(1)请写出y与x之间的关系式.
(2)当x为何值时,y有最大值,最大值是多少?此时点D在什么位置?
(3)当△ABD的面积是△ABC的面积的一半时,点D在什么位置?
(1)y=-3x+24;(2) 当x=0时,y有最大值,最大值是24,此时点D与点C重合;(3) 点D在AC的中点处 【解析】试题分析:(1)△ABD的面积=AD×BC,把相关数值代入化简即可; (2)由(1)可得x最小时,y最大,易得此时点D的位置; (3)让(1)中的y为10列式求值即可. 试题解析:(1)∵设CD=x,△ABD的面积为y. ∴y=AD×BC=×(8-x)×6...如图,在△ABC中,∠ACB=90°,AC=BC,CE⊥BE于点E,CE与AB交于点F,AD⊥CF于点D,且AD平分∠FAC.请写出图中两对全等三角形,并选择其中一对加以说明.
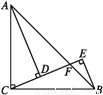
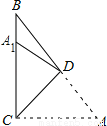
如图,已知∠AOB=α,且PC∥OB,现以P为顶点,PC为一边作∠CPD=α,并用移动三角尺的方法验证,PD与OA是否平行.
某商场为了吸引更多的顾客,安排了一个抽奖活动,并规定:顾客每购买100元商品,就能获得一次抽奖的机会.抽奖规则如下:在抽奖箱内,有100个牌子,分别写有1,2,3,…,100共100个数字,抽到末位数是5的可获20元购物券,抽到数字是88的可获200元购物券,抽到66或99的可获100元购物券.某顾客购物用了130元,他获得购物券的概率是多少?他获得20元、100元、200元购物券的概率分别是多少?
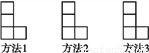
查看答案在由小正方形组成的L形的图形中,用三种不同的方法添画一个小正方形,使它成为轴对称图形.
如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律摆.
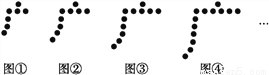
(1)第5个“广”字中的棋子个数是 .
(2)第n个“广”字需要多少枚棋子?
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案下列各式中,等号不成立的是( )
A. |﹣4|=4 B. ﹣|4|=|﹣4| C. |﹣4|=|4| D. ﹣|﹣4|=﹣4
B 【解析】试题分析:正数的绝对值等于它本身,负数的绝对值等于它的相反数,零的绝对值为零. ,则本题不成立的是B.下列式子中,正确的是( )
A. ﹣6<﹣8 B. ﹣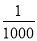 >0 C. ﹣
>0 C. ﹣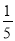 <﹣
<﹣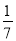 D.
D. 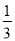 <0.3
<0.3
﹣2007的绝对值是( )
A. ﹣2007 B. ﹣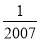 C.
C. 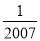 D. 2007
D. 2007
若规定收入为“+”,那么﹣50元表示( )
A.收入了50元
B.支出了50元
C.没有收入也没有支出
D.收入了100元
查看答案(1)阅读理【解析】
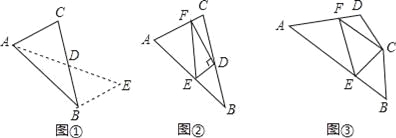
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
下面是某同学对多项式(x2﹣4x﹣3)(x2﹣4x+1)+4进行因式分解的过程.
【解析】
设x2﹣4x=y
原式=(y﹣3)(y+1)+4(第一步)
=y2﹣2y+1 (第二步)
=(y﹣1)2 (第三步)
=(x2﹣4x﹣1)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的 .
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)请你模仿以上方法尝试对多项式(x2+2x)(x2+2x+2)+1进行因式分解.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
多项式 的各项分别是( )
的各项分别是( )
A.  B.
B.  C.
C.  D.
D. 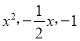
下列式子:x2+2, 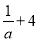 ,
, 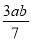 ,
, 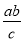 ,﹣5x,0中,整式的个数有( )
,﹣5x,0中,整式的个数有( )
A. 3个 B. 4个 C. 5个 D. 6个
查看答案我国作家莫言获得诺贝尔文学奖之后,他的代表作品《蛙》的销售量就比获奖之前增长了180倍,达到2100000册,将2100000用科学记数法表示为( )
A. 0.21×108 B. 2.1×106 C. 2.1×107 D. 21×106
查看答案两个数的和为正数,那么这两个数是( )
A. 正数 B. 负数
C. 至少有一个为正数 D. 一正一负
查看答案若|x|=4,|y|=7,且x+y>0,那么x﹣y的值是( )
A. 3或11 B. 3或﹣11 C. ﹣3或11 D. ﹣3或﹣11
查看答案数轴上一点A,一只蚂蚁从A出发爬了4个单位长度到了原点,则点A所表示的数是( )
A. 4 B. ﹣4 C. ±8 D. ±4
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一列单项式﹣x2,3x3,﹣5x4,7x5.…,按此规律排列,则第9个单项式是_____.
. 【解析】根据式子的特点,可知各项符号为:(-1)2n-1,系数为2n-1,而x的指数为n+1,因此可知其规律为:(-1)2n-1xn+1,则第9个为:(-1)2n-1(2n-1)xn+1=(-1)2×9-1(2×9-1)x9+1=-17x10. 故答案为: .在3,﹣4,6,﹣7这四个数中,任取两个数相乘,所得的积最大的是_____.
查看答案若a、b互为倒数,则(﹣ab)2017=_____.
查看答案x2+ax﹣y﹣(bx2﹣x+9y+3)的值与x的取值无关,则﹣a+b的值为( )
A. 0 B. ﹣1 C. ﹣2 D. 2
查看答案一个多项式与x2﹣3x+2的和是3x﹣1,则这个多项式为( )
A. ﹣x2+6x+1 B. ﹣x2+1 C. ﹣x2+6x﹣3 D. ﹣x2﹣6x+1
查看答案下列运算正确的是( )
A. ﹣a2b﹣2a2b=﹣3a2b B. 2a﹣a=2a
C. 3a2+2a2=5a4 D. 2a+b=2ab
查看答案 试题属性- 题型:填空题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列式子:x2+2, 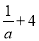 ,
, 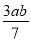 ,
, 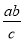 ,﹣5x,0中,整式的个数有( )
,﹣5x,0中,整式的个数有( )
A. 3个 B. 4个 C. 5个 D. 6个
B 【解析】根据整式是有理式的一部分,在有理式中可以包含加,减,乘,除四种运算,但在整式中除数不能含有字母。单项式和多项式都统称为整式。因此可知x2+2, ,﹣5x,0是整式,故有4个. 故选:B.我国作家莫言获得诺贝尔文学奖之后,他的代表作品《蛙》的销售量就比获奖之前增长了180倍,达到2100000册,将2100000用科学记数法表示为( )
A. 0.21×108 B. 2.1×106 C. 2.1×107 D. 21×106
查看答案两个数的和为正数,那么这两个数是( )
A. 正数 B. 负数
C. 至少有一个为正数 D. 一正一负
查看答案若|x|=4,|y|=7,且x+y>0,那么x﹣y的值是( )
A. 3或11 B. 3或﹣11 C. ﹣3或11 D. ﹣3或﹣11
查看答案数轴上一点A,一只蚂蚁从A 出发爬了4个单位长度到了原点,则点A所表示的数是( )
A. 4 B. 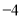 C.
C. 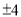 D.
D. 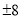
﹣2017的倒数是( )
A. 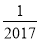 B. ﹣
B. ﹣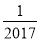 C. 2017 D. ﹣2017
C. 2017 D. ﹣2017
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律摆.

(1)第5个“广”字中的棋子个数是 .
(2)第n个“广”字需要多少枚棋子?
(1)15 (2)(2n+5)枚 【解析】试题分析:观察图形,通过归纳与总结,得到其中的规律. 试题解析:(1)由题目得:第1个“广”字中的棋子个数是7; 第2个“广”字中的棋子个数是7+(2-1)×2=9; 第3个“广”字中的棋子个数是7+(3-1)×2=11; 第4个“广”字中的棋子个数是7+(4-1)×2=13; 发现第5个“广”字中的棋子个数是7+(5-1)×2=15…...如图,点D在AB上,点E在AC上,AB=AC,AD=AE.试说明∠B=∠C.
先化简再求值:(a-2)2-(a-1)·(a+1)+5a,其中a=-2.
查看答案小聪和小明沿同一条路同时从学校出发到某图书馆查阅资料,学校与图书馆的路程是4 km,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线O—A—B—C和线段OD分别表示两人离学校的路程s(km)与所经过的时间t(min)之间的关系,请根据图象回答:下列四个结论
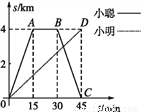
①小聪在图书馆查阅资料的时间为15 min;
②小聪返回学校的速度为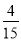 km/min;
km/min;
③小明离开学校的路程s(km)与所经过的时间t(min)之间的关系式是s=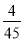 t;
t;
④当小聪与小明迎面相遇时,他们离学校的路程是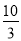 km.
km.
其中正确结论的序号是_____.
查看答案如图,△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边BC上A1处,折痕为CD,则∠A1DB=__度.
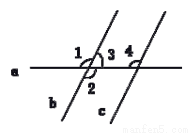
如图,∠1+∠2=284°,b∥c,则∠3= ,∠4= .
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
(2015扬州)色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
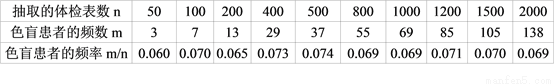
根据表中数据,估计在男性中,男性患色盲的概率为____________(结果精确到0.01)
0.07. 【解析】试题解析:观察表格发现,随着实验人数的增多,男性患色盲的频率逐渐稳定在常数0.07左右, 故男性中,男性患色盲的概率为0.07,[6a2b2+___+____]÷2ab2=3a+b-1.
查看答案在一个不透明的盒子里装有5个黑球,3个红球和2个白球,它们除颜色外其余都相同,从中随机摸出一个球,摸到红球的概率是 .
查看答案有一种原子的直径约为0.000 000 53 m,它可以用科学记数法表示为________.
查看答案如图,已知C是线段AB上的任意一点(端点除外),分别以AC,BC为边并且在AB的同一侧作等边三角形ACD和等边三角形BCE,连接AE交CD于点M,连接BD交CE于点N.给出以下三个结论:
①AE=BD;②CN=CM;③MN∥AB.其中正确结论的个数是( )
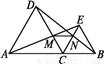
A. 0 B. 1 C. 2 D. 3
查看答案小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( ).
A. 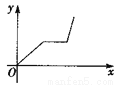 B.
B. 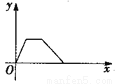 C.
C. 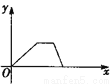 D.
D. 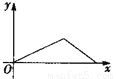
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
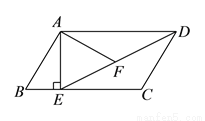
在平行四边形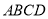 中,过点
中,过点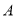 作
作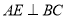 ,垂足为
,垂足为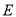 ,连接
,连接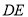 ,
, 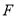 为线段
为线段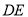 上一点,且
上一点,且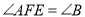 .
.
(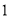 )求证:
)求证: 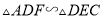 .
.
( )若
)若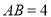 ,
, 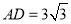 ,
, 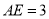 ,求
,求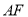 的长.
的长.
(本小题满分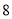 分)
分)
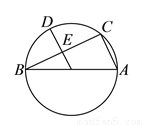
如图, 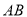 是⊙
是⊙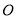 的直径,点
的直径,点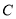 是⊙
是⊙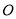 上一点,连接
上一点,连接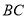 ,
, 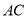 ,
, 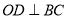 于
于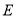 .
.
(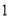 )求证:
)求证: 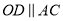 .
.
(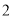 )若
)若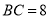 ,
, 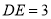 ,求⊙
,求⊙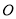 的直径.
的直径.
二次函数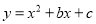 的图象经过点
的图象经过点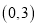 ,
, 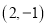 .
.
(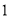 )求
)求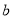 ,
, 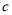 的值;
的值;
(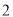 )求该二次函数图象的对称轴及与
)求该二次函数图象的对称轴及与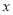 轴交点坐标.
轴交点坐标.
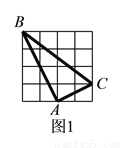
如图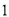 ,在
,在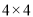 的正方形方格中,
的正方形方格中, 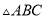 的顶点都在边长为
的顶点都在边长为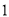 的小正方形的顶点.
的小正方形的顶点.
(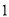 )填空:
)填空: 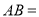 __________,
__________, 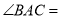 __________
__________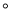 ;
;
(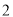 )请在图
)请在图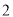 中的两个
中的两个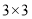 的正方形方格中各画一个和
的正方形方格中各画一个和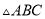 相似但不全等的格点三角形.
相似但不全等的格点三角形.

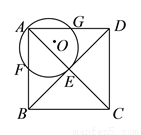
如图,在正方形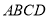 中,
中,  为对角线
为对角线 ,
, 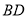 的交点,经过点
的交点,经过点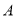 和点
和点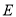 作⊙
作⊙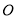 ,分别交
,分别交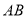 ,
, 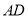 于点
于点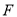 ,
, 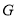 .已知正方形边长为
.已知正方形边长为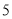 ,⊙
,⊙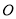 的半径为
的半径为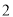 ,则
,则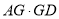 的值为__________.
的值为__________.
如图,抛物线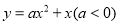 交
交 轴于点
轴于点 ,
, 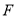 ,交
,交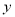 轴于点
轴于点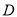 ,在
,在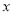 轴上方的抛物线上有两点
轴上方的抛物线上有两点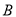 ,
, 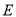 ,它们关于
,它们关于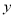 轴对称,点
轴对称,点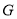 ,
, 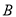 在
在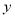 轴左侧,
轴左侧, 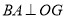 于点
于点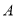 ,
, 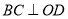 于点
于点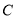 ,四边形
,四边形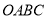 与四边形
与四边形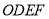 的面积分别为
的面积分别为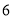 和
和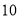 ,则
,则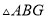 与
与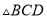 的面积之和为__________.
的面积之和为__________.
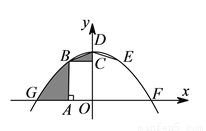
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一副三角板如图叠放在一起,则图中∠α的度数为( )
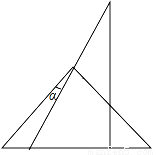
A. 35° B. 30° C. 25° D. 15°
D 【解析】如图,根据三角板角度的特殊性可知∠1=45°,∠2=60°,根据三角形外角的性质可得∠α=∠2-∠1=60°-45°=15°.故选D.如图,EA∥DF,AE=DF,要使△AEC≌△DFB,只要( )
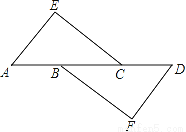
A. AB=CD B. EC=BF C. ∠A=∠D D. AB=BC
查看答案如图,已知在△ABC中,∠ABC=70°,∠C=50°,BD是角平分线,则∠BDC的度数为
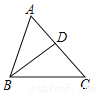
A. 95° B. 100° C. 110° D. 120°
查看答案三条线段a=5,b=3,c的值为整数,由a、b、c为边可组成三角形( )
A. 1个 B. 3个 C. 5个 D. 无数个
查看答案在下列四个交通标志图中,是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
已知实数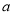 ,
, 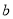 满足:
满足: 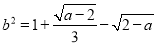 ,且
,且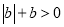 ,求
,求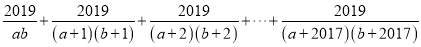 的值.
的值.
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

