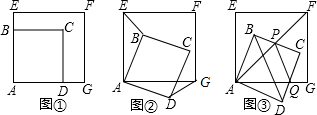
题目内容
将正方形ABCD绕中心O顺时针旋转角 得到正方形
得到正方形 ,如图1所示.
,如图1所示.
1.当 =45
=45 时(如图2),若线段
时(如图2),若线段 与边
与边 的交点为
的交点为 ,线段
,线段 与
与 的交点为
的交点为 ,可得下列结论成立
①
,可得下列结论成立
① ;②
;② ,试选择一个证明.
,试选择一个证明.
2.当 时,第(1)小题中的结论
时,第(1)小题中的结论 还成立吗?如果成立,请证明;如果不成立,请说明理由
还成立吗?如果成立,请证明;如果不成立,请说明理由
3.在旋转过程中,记正方形 与AB边相交于P,Q两点,探究
与AB边相交于P,Q两点,探究 的度数是否发生变化?如果变化,请描述它与
的度数是否发生变化?如果变化,请描述它与 之间的关系;如果不变,请直接写出
之间的关系;如果不变,请直接写出 的度数.
的度数.

【答案】
1.

2.


3.在旋转过程中, 的度数不发生变化
的度数不发生变化

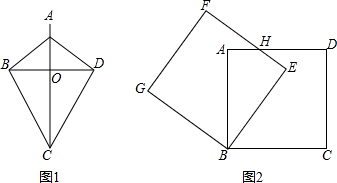
【解析】(1)①根据旋转的性质可得:∠AOA1=45°,即可证明∠PFO=90°,则OE=OF,即可根据HL公理证明两三角形全等;②先证明△EOP≌△FOP,再证明∴△APO≌△A1PO,即可证得;
(2)作OE⊥A1D1,OF⊥AB,垂足分别为E,F,首先△EOP≌△FOP证得∠APO=∠A1PO,即可证明△APO≌△A1PO,从而结论得证;
(3)根据(1)(2)的解题过程中∠POQ的大小不变,即可确定.

练习册系列答案
相关题目
 11、正方形ABCD在平面直角坐标系中的位置如图,将正方形ABCD绕D点顺时针方向旋转90°后,B点到达的位置坐标为( )
11、正方形ABCD在平面直角坐标系中的位置如图,将正方形ABCD绕D点顺时针方向旋转90°后,B点到达的位置坐标为( ) 如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.正方形ABCD顶点都在格点上,其中,点A的坐标为(1,1).
如图,在平面直角坐标系中,O为坐标原点,每个小方格的边长为1个单位长度.正方形ABCD顶点都在格点上,其中,点A的坐标为(1,1). (2008•烟台)正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针方向旋转90°后,B点到达的位置坐标为( )
(2008•烟台)正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针方向旋转90°后,B点到达的位置坐标为( )