题目内容
7.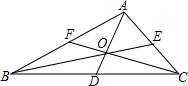 如图,已知△ABC的周长为36cm,BE,CF分别为边AC,AB上的中点,BE,CF相交于点O,AO的延长线交BC于点D,且AF=6cm,AE=4cm,求BD的长.
如图,已知△ABC的周长为36cm,BE,CF分别为边AC,AB上的中点,BE,CF相交于点O,AO的延长线交BC于点D,且AF=6cm,AE=4cm,求BD的长.
分析 先由BE、CF分别为AC、AB边上的中线,得出AB=2AF=12cm,AC=2AE=8cm,再根据△ABC的周长为36cm,求出BC=16cm,又三角形的三条中线相交于同一点,则BD=$\frac{1}{2}$BC=8cm.
解答 解:∵BE、CF分别为AC、AB边上的中线,
∴AB=2AF=12cm,AC=2AE=8cm.
∵△ABC的周长为36cm,
∴AB+BC+AC=36cm,
∴BC=16cm.
∵三角形的三条中线相交于同一点,
∴AD是BC边上的中线,
∴BD=$\frac{1}{2}$BC=8cm.
点评 本题考查了三角形的中线的定义与性质,三角形的周长,难度适中.掌握三角形的三条中线相交于同一点是解题的关键.

练习册系列答案
相关题目
2.某校九年级(1)、(2)班的全体学生进行跳绳体育测试,并从每班随机选取6名学生的测试成绩(单位:个)如下表:
(1)分别求九年级(1)、(2)两班随机选取6名学生的测试成绩的中位数;
(2)若只看九年级(1)、(2)两班随机选取的这6名学生,哪个班级的测试成绩更稳定?
(3)求九年级(1)、(2)班全体学生跳绳测试成绩的方差的估计值.
| 学生 | 1 | 2 | 3 | 4 | 5 | 6 |
| (1)班的成绩/个 | 77 | 81 | 74 | 84 | 78 | 80 |
| (2)班的成绩/个 | 79 | 77 | 80 | 77 | 79 | 82 |
(2)若只看九年级(1)、(2)两班随机选取的这6名学生,哪个班级的测试成绩更稳定?
(3)求九年级(1)、(2)班全体学生跳绳测试成绩的方差的估计值.
12.下列四组数中,能作为直角三角形三边长的是( )
| A. | 8,15,17 | B. | 4,5,6 | C. | 2,3,4 | D. | 1,$\sqrt{2},3$ |
19.下列图象不能表示变量y是变量x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
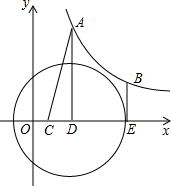 如图所示:点A,B是反比例函数y=$\frac{k}{x}$(x>0)图象上的两个动点,分别过点A、B点作AD⊥x轴于D,BE⊥x轴于E,点C是线段OD的中点.
如图所示:点A,B是反比例函数y=$\frac{k}{x}$(x>0)图象上的两个动点,分别过点A、B点作AD⊥x轴于D,BE⊥x轴于E,点C是线段OD的中点. 如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC等于8.
如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC等于8.