题目内容
 如图,AD、CD是△ABC两个外角的角平分线,若∠BAC=60°,∠BCA=80°,则∠B=________°,∠D=________°.
如图,AD、CD是△ABC两个外角的角平分线,若∠BAC=60°,∠BCA=80°,则∠B=________°,∠D=________°.
40 70
分析:先根据三角形的内角和求∠B的度数,在根据外角的定义,求∠EAC和∠ACF,再根据角平分线的定义和三角形的内角和求∠D的度数.
解答:∵∠BAC=60°,∠BCA=80°
∴∠B=180°-∠BAC-∠BCA=180°-60°-80°=40°
∴∠EAC=120°,∠ACF=100°
∵AD、CD是△ABC两个外角的角平分线
∴∠DAC= ∠EAC=60°,∠ACD=
∠EAC=60°,∠ACD= ∠ACF=50°
∠ACF=50°
在△ACD中,∠D=180°-∠DAC-∠ACD=70°.
故答案为40、70.
点评:正确理解三角形的外角与相邻的内角互补,结合三角形的内角和和角平分线的定义是解决此类问题的关键.
分析:先根据三角形的内角和求∠B的度数,在根据外角的定义,求∠EAC和∠ACF,再根据角平分线的定义和三角形的内角和求∠D的度数.
解答:∵∠BAC=60°,∠BCA=80°
∴∠B=180°-∠BAC-∠BCA=180°-60°-80°=40°
∴∠EAC=120°,∠ACF=100°
∵AD、CD是△ABC两个外角的角平分线
∴∠DAC=
 ∠EAC=60°,∠ACD=
∠EAC=60°,∠ACD= ∠ACF=50°
∠ACF=50°在△ACD中,∠D=180°-∠DAC-∠ACD=70°.
故答案为40、70.
点评:正确理解三角形的外角与相邻的内角互补,结合三角形的内角和和角平分线的定义是解决此类问题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
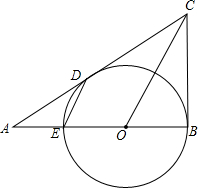 如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接OC,ED.
如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接OC,ED. 如图,AD、CD是△ABC两个外角的角平分线,若∠BAC=60°,∠BCA=80°,则∠B=
如图,AD、CD是△ABC两个外角的角平分线,若∠BAC=60°,∠BCA=80°,则∠B= 17、如图,AB,CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是
17、如图,AB,CD是⊙O的两条弦,它们相交于点P,连接AD、BD,已知AD=BD=4,PC=6,那么CD的长是 如图:已知CD是直角三角形ABC的斜边上的高,且AD=8,BD=2,则BC=
如图:已知CD是直角三角形ABC的斜边上的高,且AD=8,BD=2,则BC=