题目内容
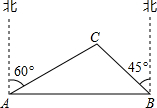 如图,台风过后,海警迅速救援,正在基地A的正东方向距离A地40海里的B处海警接到命令,要求前往C岛,接送伤员.以知C岛在A岛的北偏东60度方向,且在B岛的北偏西45度方向.B处海警出发,平均每小时行二十海里需多长时间才能把伤员送到A处救治?
如图,台风过后,海警迅速救援,正在基地A的正东方向距离A地40海里的B处海警接到命令,要求前往C岛,接送伤员.以知C岛在A岛的北偏东60度方向,且在B岛的北偏西45度方向.B处海警出发,平均每小时行二十海里需多长时间才能把伤员送到A处救治?考点:解直角三角形的应用-方向角问题
专题:
分析:作CD⊥AB于D点.设CD=x海里,在直角△ACD中,利用x表示出AC,AD,同理表示出BD,BC,根据AB=40即可列出方程求得CD的长,则AC+CB即可求得,然后除以速度即可得到时间.
解答:解:作CD⊥AB于D点.设CD=x海里,
在直角△ACD中,∠CAD=90°-60°=30°,
则AC=2x,AD=
x,
在直角△BCD中,∠CBD=45°,
则BD=CD=x,BC=
CD=
x,
∵AB=40,即AD+BD=40,
∴
x+x=40,
解得:x=20(
-1),
∴BC=20
(
-1)=20
-20
,AC=2x=40(
-1),
则总路程是:20
-20
+40(
-1)海里,
则时间是:
=
-
+2
-2≈2.45-1.41+2×1.73-2≈2.5(小时).
答:需要2.5小时能把伤员送到A处救治.

在直角△ACD中,∠CAD=90°-60°=30°,
则AC=2x,AD=
| 3 |
在直角△BCD中,∠CBD=45°,
则BD=CD=x,BC=
| 2 |
| 2 |
∵AB=40,即AD+BD=40,
∴
| 3 |
解得:x=20(
| 3 |
∴BC=20
| 2 |
| 3 |
| 6 |
| 2 |
| 3 |
则总路程是:20
| 6 |
| 2 |
| 3 |
则时间是:
20
| ||||||
| 20 |
| 6 |
| 2 |
| 3 |
答:需要2.5小时能把伤员送到A处救治.
点评:本题主要考查了方向角含义,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )| A、5cm | B、10cm |
| C、15cm | D、17.5cm |
下列说法中错误的是( )
| A、近似数0.8与0.80表示的意义不同 |
| B、近似数0.3000精确到万分位 |
| C、49554精确到万位是49000 |
| D、3.145×104是精确到十位的近似数 |

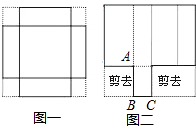 小明与小王在课题学习时分别要把两块边长都为12cm的正方形纸片要制作成两个无盖的长方体盒子(不计粘合部分),方案如下:
小明与小王在课题学习时分别要把两块边长都为12cm的正方形纸片要制作成两个无盖的长方体盒子(不计粘合部分),方案如下: 某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线是抛物线y=-x2+4x(单位:米)的一部分.则水喷出的最大高度是
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线是抛物线y=-x2+4x(单位:米)的一部分.则水喷出的最大高度是