题目内容
如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,则图中阴影部分的面积为_________.(结果保留π)

 .
.
【解析】
试题分析:连接OC,由AB为圆的切线,得到OC垂直于AB,再由OA=OB,利用三线合一得到C为AB中点,且OC为角平分线,在直角三角形AOC中,利用30度所对的直角边等于斜边的一半求出OC的长,利用勾股定理求出AC的长,进而确定出AB的长,求出∠AOB度数,阴影部分面积=三角形AOB面积-扇形面积,求出即可.
试题解析:连接OC,

∵AB与圆O相切,
∴OC⊥AB,
∵OA=OB,
∴∠AOC=∠BOC,∠A=∠B=30°,
在Rt△AOC中,∠A=30°,OA=4,
∴OC= OA=2,∠AOC=60°,
OA=2,∠AOC=60°,
∴∠AOB=120°,AC= ,
,
即AB=2AC=4 ,
,
则S阴影=S△AOB-S扇形= .
.
考点:1.切线的性质;2.含30度角的直角三角形;3.扇形面积的计算.

练习册系列答案
相关题目



 B.13π C.25π D.25
B.13π C.25π D.25
 B.k≥-
B.k≥-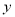 ,下列图象中,能表示
,下列图象中,能表示 与
与 的函数关系的图象大致是( )
的函数关系的图象大致是( )
 B.
B. C.
C. D.
D.
 为原点,
为原点, 、
、 两点坐标分别为
两点坐标分别为 、
、 .
.
 为位似中心在
为位似中心在 轴左侧将
轴左侧将 放大为原来的两倍,并画出图形;
放大为原来的两倍,并画出图形; ,
, 两点的对应点
两点的对应点 ,
,  的坐标;
的坐标; 为
为 ,点
,点 内的对应点为
内的对应点为 ,
, 的长;
的长; 为
为 的内心,则
的内心,则 度.
度.