Question

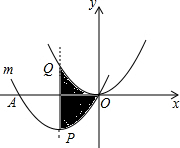如图，把抛物线y=

1

2

x²平移得到抛物线m，抛物线m经过点A（-6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y=

1

2

x²交于点Q，则图中阴影部分的面积为（　　）

• A、9
• B、

  27

  2

• C、

  25

  3

• D、

  21

  2

Answer 1

考点：二次函数图象与几何变换

专题：

分析：先利用配方法得到抛物线m：y=

1

2

（x+6）x=

1

2

（x+3）²-

9

2

的顶点坐标为（-3，-

9

2

），则抛物线y=

1

2

x²向左平移3个单位，向下平移

9

2

个单位得到抛物线y=

1

2

x²+6x，然后利用阴影部分的面积等于△POQ面积进行计算．

解答：解：根据题意知，抛物线m的解析式为y=

1

2

（x+6）x=

1

2

（x+3）²-

9

2

，
则抛物线m的顶点坐标为（-3，-

9

2

），
所以抛物线y=

1

2

x²向左平移3个单位，向下平移

9

2

个单位得到抛物线m，
所以对称轴与两抛物线所围成的阴影部分的面积=

1

2

×3×9=

27

2

．
故选：B．

点评：本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．