题目内容
18.利用描点法画出函数y=2x-3的图象.(1)判断点A(-3.5,-10.5),B(2.5,2),C(4,6)是否在函数y=2x-3的图象上.
(2)观察图象,找出函数值y随自变量x的变化规律.
分析 根据描点法,可得函数图象;
根据点的坐标满足函数解析式,点在函数图象上,点的坐标不满足函数解析式,点不再函数图象上;
根据一次函数的性质,可得答案.
解答 解:如图: ;
;
(1)当x=-3.5时,y=2×(-3.5)-3=-10≠-10.5,故A(-3.5,-10.5)不再函数图象上,
当x=2.5时,y=2×2.5-3=2,故B(2.5,2)在函数图象上;
当x=4时,y=2×4-3=5≠6,故C不再函数图象上;
(2)k=2>0,函数值y随自变量x的增大而增大.
点评 本题考查了一次函数图象,利用了点与图象的关系:点的坐标满足函数解析式,点在函数图象上,点的坐标不满足函数解析式,点不再函数图象上;一次函数的性质:k>0,y随x的增大而增大,k<0,y随x的增大而减小.

练习册系列答案
相关题目
10.在-1,0,3和$\sqrt{2}$这四个实数中,负数是( )
| A. | -1 | B. | 0 | C. | 3 | D. | $\sqrt{2}$ |
10.下列各组单项式中,不是同类项的是( )
| A. | -2与5 | B. | 6a2mb与-a2bm | C. | 2abx3与$-\frac{5}{6}ba{x^3}$ | D. | $\frac{1}{2}{x^3}y$与$-\frac{1}{2}x{y^3}$ |
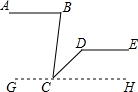 把下列解题补充完整:
把下列解题补充完整: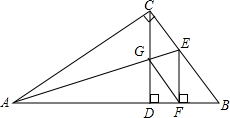 如图,AC⊥BC,AE平分∠CAB,CD⊥AB,EF⊥AB,连接FG,求证:CEFG为菱形.
如图,AC⊥BC,AE平分∠CAB,CD⊥AB,EF⊥AB,连接FG,求证:CEFG为菱形.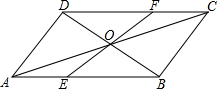 E,F分别是?ABCD的边AB,CD上的一点,且DF=BE,O是BD的中点,EF过点O.求证:EF与AC互相平分.
E,F分别是?ABCD的边AB,CD上的一点,且DF=BE,O是BD的中点,EF过点O.求证:EF与AC互相平分.