题目内容
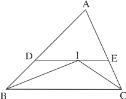
【题目】如图，在△ABC中，∠B与∠C的角平分线相交于点I，过点I作BC的平行线，分别交AB、AC于点D、E.若AB=9,AC=6，BC=8，则△ADE的周长是（ ）
A. 14B. 15C. 17D. 23
【答案】B
【解析】
根据角平分线的定义得∠DBI=∠CBI，∠ECI=∠BCI，再根据平行线的性质得∠DFB=∠CBI，∠BCI=∠EIC，则∠DBI=∠DIB，∠ECI=∠EIC，根据平行线的判定得DB=DI，EI=EC，再根据三角形的定义得△ADE的周长= AD+DE+AE=AD+DI+AE+EI=AD+DB+AE+CE=AB+AC
∵BI、CI分别平分∠ABC和∠ACB，
∴∠ABI=∠CBI，∠ACI=∠BCI.
∵DE∥BC，
∴∠DIB=∠IBC，∠BCI=∠EIC.
∴∠ABI=∠DIB，∠EIC=∠ACI.
∴DB=DI，EI=EC.
∴L△ADE=AD+DE+AE=AD+DI+AE+EI=AD+DB+AE+CE=AB+AC=9+6=15.
故选：B.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
