题目内容
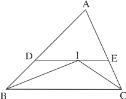
【题目】探索与证明:
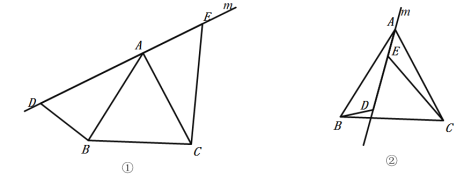
(1)如图①,直线![]() 经过正三角形
经过正三角形![]() 的顶点
的顶点![]() ,在直线
,在直线![]() 上取点
上取点![]() ,
,![]() ,使得
,使得![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明;
之间满足的数量关系,并予以证明;
(2)将(1)中的直线![]() 绕着点
绕着点![]() 逆时针方向旋转一个角度到如图②的位置,
逆时针方向旋转一个角度到如图②的位置,![]() ,
,![]() .通过观察或测量,猜想线段
.通过观察或测量,猜想线段![]() ,
,![]() 与
与![]() 之间满足的数量关系,并予以证明.
之间满足的数量关系,并予以证明.
【答案】(1)DE=BD+CE,证明见解析;(2)CE =BD+DE,证明见解析
【解析】
(1)根据等边三角形的性质可得AB=CA,∠BAC=60°,然后根据已知条件可得![]() ,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据DE=AE+AD和等量代换即可得出结论;
,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据DE=AE+AD和等量代换即可得出结论;
(2)根据等边三角形的性质可得AB=CA,∠BAC=60°,然后根据已知条件可得![]() ,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据AD= AE+DE和等量代换即可得出结论;
,并且可证出∠ABD=∠CAE,利用AAS即可证出△ABD≌△CAE,从而得出BD=AE,AD= CE,然后根据AD= AE+DE和等量代换即可得出结论;
解:(1)DE=BD+CE,证明如下
∵△ABC为等边三角形
∴AB=CA,∠BAC=60°
∵![]() ,
,![]()
∴![]()
∴∠ABD+∠BAD=180°-∠ADB=120°
∠CAE+∠BAD=180°-∠BAC=120°
∴∠ABD=∠CAE
在△ABD和△CAE中
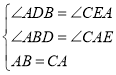
∴△ABD≌△CAE
∴BD=AE,AD= CE
∴DE=AE+AD= BD+CE;
(2)CE =BD+DE,证明如下
∵△ABC为等边三角形
∴AB=CA,∠BAC=60°
∵![]() ,
,![]()
∴![]()
∴∠ABD+∠BAD=180°-∠ADB=60°
∠CAE+∠BAD=∠BAC=60°
∴∠ABD=∠CAE
在△ABD和△CAE中
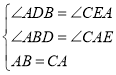
∴△ABD≌△CAE
∴BD=AE,AD= CE
∵AD= AE+DE
∴CE= BD+DE.

【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题
![]() 求表中a的值;
求表中a的值;![]() 频数分布直方图补充完整;
频数分布直方图补充完整;
![]() 小亮想根据此直方图绘制一个扇形统计图,请你帮他算出成绩为
小亮想根据此直方图绘制一个扇形统计图,请你帮他算出成绩为![]() 这一组所对应的扇形的圆心角的度数;
这一组所对应的扇形的圆心角的度数;
![]() 若测试成绩不低于80分为优秀,则本次测试的优秀率
若测试成绩不低于80分为优秀,则本次测试的优秀率![]() 百分比
百分比![]() 是多少?
是多少?