Question

如图，BD、CE是△ABC的中线，G、H分别是BE、CD的中点，BC=8，求GH的长．

Answer 1

分析：GH是梯形EBCD的中位线，DE是△ABC的中位线，根据中位线定理就可以求出．

解答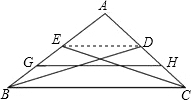：解法一：连接DE
∵AE=EB，AD=DC
∴DE∥BC，DE=

1

2

BC=

1

2

×8=4，
又∵EG=GB，DH=HC
∴GH=

1

2

（ED+BC）=

1

2

（4+8）=6．
解法二：∵E、D分别是AB、AC的中点，G、H分别是EB、DC的中点
∴

AG

AB

=

AH

AC

=

3

4

，
∴△AGH∽△ABC，
∴

GH

BC

=

AC

AB

=

3

4

，
∴GH=

3

4

×8=6．

点评：本题主要考查了三角形的中位线定理，和梯形的中位线定理．