��Ŀ����
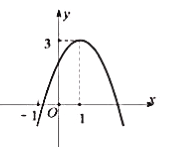
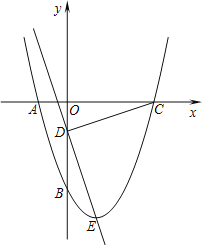
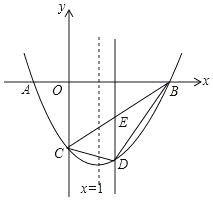
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��C������ֱ�Ϊ(1,0)��(0,3)����B��x���ϣ���֪ij���κ�����ͼ��A�� B��C���㣬�����ĶԳ���Ϊֱ��x=1����DΪֱ��BC�·��Ķ��κ�����ͼ���ϵ�һ������(��D��B��C���غ�)������D��y���ƽ���߽�BC�ڵ�E��
(1)��ö��κ����Ľ���ʽ��
(2)���D�ĺ�����Ϊm���ú�m�Ĵ���ʽ��ʾ�߶�DE�ij���
(3)���DBC��������ֵ���������ʱ��D�����꣮
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() ��D
��D![]() ��
��
��������
��1���ô���ϵ��������κ�������ʽ��
��2������ֱ��BC�Ľ���ʽ����m�ֱ����ֱ��BC�Ͷ��κ����Ľ���ʽ�����E��D�������꣬�ɴ�����߶�DE��
��3����������ͣ�S��DBC=S��BEB+S��DEB=![]() ��OBһ����������DBC��������ֵ��DE�������ݴ���⣮
��OBһ����������DBC��������ֵ��DE�������ݴ���⣮
��1������κ����Ľ���ʽΪ![]() Ϊ����)���������߶Գ���֪B������Ϊ(3,0)���ֱ�A(1,0)��B(3,0)��C(0,3)�������ʽ�ã�
Ϊ����)���������߶Գ���֪B������Ϊ(3,0)���ֱ�A(1,0)��B(3,0)��C(0,3)�������ʽ�ã�
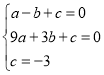
��ã�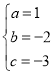
�ʸö��κ����Ľ���ʽΪ![]() ��
��
��2����ֱ��BC�Ľ���ʽΪ![]() �dz���)����B(3,0)��C(0,-3)����ã�
�dz���)����B(3,0)��C(0,-3)����ã�
![]()
��ã�![]()
��BC�Ľ���ʽΪ![]()
��![]()
![]()
![]() )
)
��DE=![]()
��3��S��DBC=S��BEB+S��DEB
=![]()
=![]()
=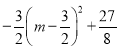
��![]() ʱ����DBC��������Ϊ
ʱ����DBC��������Ϊ![]()
��![]() ����
����![]() ����
����![]() ��
��
���D������Ϊ![]() ��
��

 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д�����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ��ijУ�ٰ�������������д��������ѧ����ѡ�κ�������������ͬʱ��д100�����֣�ÿ��ȷ��д��һ�����ֵ�1�֣����ξ�����ѧ���ɼ�Ϊ![]() ���֣�����
���֣�����![]() �����䰴�����η�Ϊ���飬���Ƴ����²���������
�����䰴�����η�Ϊ���飬���Ƴ����²���������
��� | �ɼ� | Ƶ���������� | Ƶ�� |
һ |
| 2 | 0.04 |
�� |
| 10 | 0.2 |
�� |
| 14 | b |
�� |
| a | 0.32 |
�� |
| 8 | 0.16 |
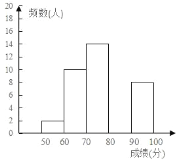
����ݱ����ṩ����Ϣ������������⣺
��1�����ξ�������________��ѧ���μӣ�
��2��ֱ��д������![]() _________��
_________��![]() _________��
_________��
��3���벹ȫ������Ӧ��Ƶ���ֲ�ֱ��ͼ��
��4���������ɼ�������80��Ϊ���㣬�δ�����������Ϊ_________��