题目内容
如图Ⅰ，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1、S2、S3表示，则不难证明S1=S2+S3．
（1）如图Ⅱ，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1、S2、S3表示，设BC=a，AC=b，AB=c，证明：S1=S2+S3．
（2）如图Ⅲ，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1、S2、S3之间的关系．（不必证明）
（3）若分别以直角三角形ABC三边为边向外作三个正多边形，其面积分别用S1、S2、S3表示，请你猜想S1、S2、S3之间的关系？．（不必证明）
（1）如图Ⅱ，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1、S2、S3表示，设BC=a，AC=b，AB=c，证明：S1=S2+S3．
（2）如图Ⅲ，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1、S2、S3之间的关系．（不必证明）
（3）若分别以直角三角形ABC三边为边向外作三个正多边形，其面积分别用S1、S2、S3表示，请你猜想S1、S2、S3之间的关系？．（不必证明）
分析：（1）分别用AB、BC和AC表示出 S1、S2、S3，然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系；
（2）分别用AB、BC和AC表示出 S1、S2、S3，然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系；
（3）分别用AB、BC和AC表示出 S1、S2、S3，然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系．
（2）分别用AB、BC和AC表示出 S1、S2、S3，然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系；
（3）分别用AB、BC和AC表示出 S1、S2、S3，然后根据AB2=AC2+BC2即可得出S1、S2、S3的关系．
解答：解：（1）∵S3=
AC2，S2=
BC2，S1=
AB2，
∴
AC2+
BC2=
AB2，
即
b2+
a2=
c2，
在Rt△ABC中，
∵b2+a2=c2，
∴S2+S3=S1．
（2）S1=S2+S3．
理由：由题意可得出：S1=
AB2，S2=
BC2，S3=
AC2，
∴则S1=
c2，S2=
a2，S3=
b2
∴S2+S3=
（a2+b2）=
c2=S1，
即S1=S2+S3．
（3）由（1）（2）可得出：S1=S2+S3．
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
∴
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
即
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
在Rt△ABC中，
∵b2+a2=c2，
∴S2+S3=S1．
（2）S1=S2+S3．
理由：由题意可得出：S1=
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
∴则S1=
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
∴S2+S3=
| ||
| 4 |
| ||
| 4 |
即S1=S2+S3．
（3）由（1）（2）可得出：S1=S2+S3．
点评：此题主要考查了三角形、正方形、圆的面积计算以及勾股定理的应用，解题关键是熟练掌握勾股定理的公式，难度一般．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
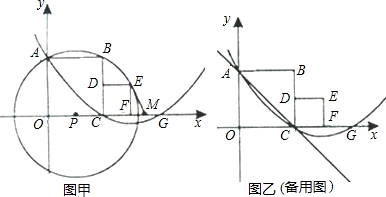
经过A、C两点，与x轴的另一交点为G，M是FG的中点，正方形CDEF的面积为1。
