题目内容
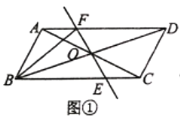
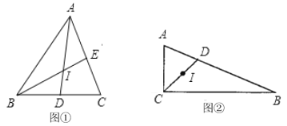
【题目】（1）如图①，小明同学作出
两条角平分线
，
得到交点
，就指出若连接
，则平分
，你觉得有道理吗？为什么？
（2）如图②，
中，
，
，
，的角平分线
上有一点，设点到边
的距离为
.（为正实数）
小季、小何同学经过探究，有以下发现：
小季发现：的最大值为
.
小何发现：当
时，连接
，则平分
.
请分别判断小季、小何的发现是否正确？并说明理由.
【答案】（1）有道理，理由详见解析；（2）小季和小何都正确，理由详见解析
【解析】
（1）过I点分别作IM，IN，IK垂直于AB，BC，AC于点M，N，K，根据角平分线的性质即可得解；
（2）根据等积法的相关方法进行求解即可.
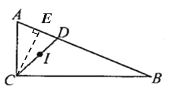
（1）如下图，过I点分别作IM，IN，IK垂直于AB，BC，AC于点M，N，K，连接IC
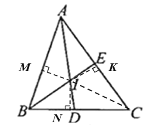
∵AI平分∠BAC，IM⊥AB，IK⊥AC
∴IM=IK，同理IM=IN
∴IK=IN
又∵IK⊥AC，IN⊥BC
∴CI平分∠BCA；
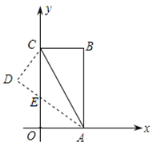
（2）如下图，过C点作CE⊥AB于点E，则d的最大值为CE长
∵
，
∴
又∵
∴
∴
的最大值为
∴小季正确；
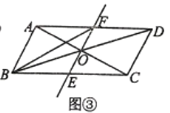
假设此时
平分
，如下图，连接AI，BI，过I点作IG，IH，IF分别垂直于AC，BC，AB于点G，H，F
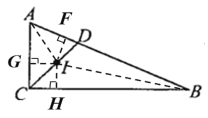
∵AI平分，CD平分∠ACB
∴BI平分∠CBA
∵IG⊥AC，IH⊥BC，ID⊥AB
∴IG=IH=IF=d
∵
∴
∴
∴
∴假设成立，当时，连接，则平分
∴小何正确.
练习册系列答案
相关题目
