题目内容
如图,在等腰梯形ABCD中,ABDC,AB=3 ,DC=
,DC= ,高CE=2
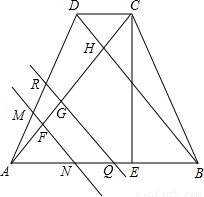
,高CE=2 ,对角线AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
,对角线AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.
(1)填空:∠AHB= ;AC= ;
(2)若S2=3S1,求x;
(3)设S2=mS1,求m的变化范围.
解:(1)90°;4。
(2)直线移动有两种情况:0<x< 及
及 ≤x≤2。
≤x≤2。
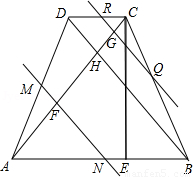
①当0<x< 时,∵MN∥BD,∴△AMN∽△ARQ。
时,∵MN∥BD,∴△AMN∽△ARQ。
∵直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,
∴△AMN和△ARQ的相似比为1:2。
∴ 。∴S2=4S1,与题设S2=3S1矛盾。
。∴S2=4S1,与题设S2=3S1矛盾。
∴当0<x< 时,不存在x使S2=3S1。
时,不存在x使S2=3S1。
②当 ≤x≤2时,
≤x≤2时,
∵AB∥CD,∴△ABH∽△CDH。
∴CH:AH=CD:AB=DH:BH=1:3。
∴CH=DH= AC=1,AH═BH=4﹣1=3。
AC=1,AH═BH=4﹣1=3。
∵CG=4﹣2x,AC⊥BD,∴S△BCD= ×4×1=2
×4×1=2
∵RQ∥BD,∴△CRQ∽△CDB。
∴ 。
。
又 ,
,
∵MN∥BD,∴△AMN∽△ADB。∴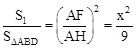 ,
,
∴S1= x2,S2=8﹣8(2﹣x)2。
x2,S2=8﹣8(2﹣x)2。
∵S2=3S1,∴8﹣8(2﹣x)2=3· x2,解得:x1=
x2,解得:x1= (舍去),x2=2。
(舍去),x2=2。
∴x的值为2。
(3)由(2)得:当0<x< 时,m=4,
时,m=4,
当 ≤x≤2时,∵S2=mS1,
≤x≤2时,∵S2=mS1,
∴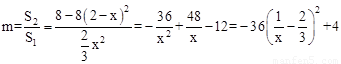 。
。
∴m是 的二次函数,当
的二次函数,当 ≤x≤2时,即当
≤x≤2时,即当 时,m随
时,m随 的增大而增大,
的增大而增大,
∴当x= 时,m最大,最大值为4;当x=2时,m最小,最小值为3。
时,m最大,最大值为4;当x=2时,m最小,最小值为3。
∴m的变化范围为:3≤m≤4。
【解析】相似三角形的判定和性质,平移的性质,二次函数的最值,等腰梯形的性质。
【分析】(1)过点C作CK∥BD交AB的延长线于K,
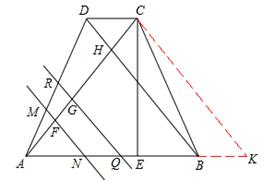
∵CD∥AB,∴四边形DBKC是平行四边形。
∴BK=CD=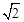 ,CK=BD。
,CK=BD。
∴AK=AB+BK= 。
。
∵四边形ABCD是等腰梯形,∴BD=AC。
∴AC=CK。∴AE=EK= AK=2
AK=2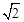 =CE。
=CE。
∵CE是高,∴∠K=∠KCE=∠ACE=∠CAE=45°。∴∠ACK=90°。∴∠AHB=∠ACK=90°
∴AC=AK•cos45°= 。
。
(2)直线移动有两种情况:0<x< 及
及 ≤x≤2;然后分别从这两种情况分析求解:当
≤x≤2;然后分别从这两种情况分析求解:当
0<x< 时,易得S2=4S1≠3S1;当
时,易得S2=4S1≠3S1;当 ≤x≤2时,根据相似三角形的性质与直角三角形的面积的求解方法,可求得△BCD与△CRQ的面积,继而可求得S2与S1的值,由S2=3S1,即可求得x的值;
≤x≤2时,根据相似三角形的性质与直角三角形的面积的求解方法,可求得△BCD与△CRQ的面积,继而可求得S2与S1的值,由S2=3S1,即可求得x的值;
(3)由(2)可得当0<x< 时,m=4;当
时,m=4;当 ≤x≤2时,可得
≤x≤2时,可得 ,化为关于
,化为关于 的二次函数
的二次函数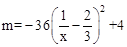 ,利用二次函数的性质求得m的变化范围。
,利用二次函数的性质求得m的变化范围。

 在,求出这样的t的值;若不存在,请说明理由.
在,求出这样的t的值;若不存在,请说明理由. 10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE.
10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE. 已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD.
已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD. (2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
(2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
