题目内容
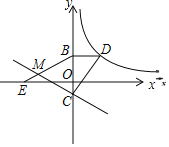
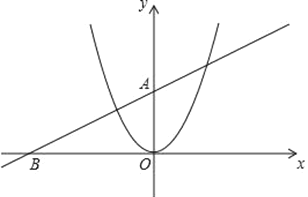
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
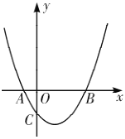
(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)在直线![]() 下方的抛物线上是否存在一点
下方的抛物线上是否存在一点![]() ,使
,使![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,C
,C![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]()
【解析】
(1)由待定系数法即可解决问题;
(2)求出点D、B坐标,理由待定系数法可解;
(3)如图,作PE∥y轴交BD于E,设P(m,![]() ),则E(m,
),则E(m,![]() m+2),构建二次函数,利用二次函数的性质即可解决问题;
m+2),构建二次函数,利用二次函数的性质即可解决问题;
解(1)解方程![]() ,得
,得![]() ,
,![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() 点坐标为
点坐标为![]() .
.
(2)∵点![]() 与点
与点![]() 关于
关于![]() 轴对称,∴
轴对称,∴![]() 点坐标为
点坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,解得
,解得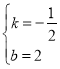 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(3)如图作![]() 轴交
轴交![]() 于
于![]() ,
,
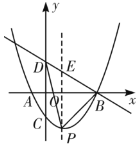
设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 的面积最大,面积的最大值为9,
的面积最大,面积的最大值为9,
此时,![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
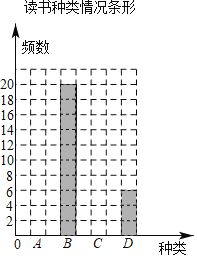
【题目】寒假中,某校七年级开展“阅读经典,读一本好书”的活动.为了解学生阅读情况,从全年级学生中随机抽取了部分学生调查读书种类情况,并进行统计分析,绘制了如下不完整的统计图表:
读书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | a | 32% |
B.文学类 | 20 | 40% |
C.艺术类 | 8 | b |
D.其他类 | 6 | 12% |
请根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)若绘制“阅读情况扇形统计图”,则“艺术类”所对应扇形的圆心角度数为 °;
(3)若该校七年级共有800人,请估计全年级在本次活动中读书种类为“艺术类”的学生人数.