Question

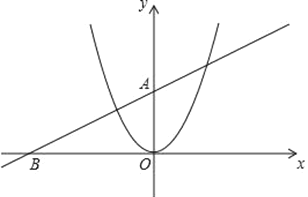
【题目】已知直线y＝kx+b经过点A（0，2），B（﹣4，0）和抛物线y＝x2．

（1）求直线的解析式；

（2）将抛物线y＝x2沿着x轴向右平移，平移后的抛物线对称轴左侧部分与y轴交于点C，对称轴右侧部分抛物线与直线y＝kx+b交于点D，连接CD，当CD∥x轴时，求平移后得到的抛物线的解析式；

（3）在（2）的条件下，平移后得到的抛物线的对称轴与x轴交于点E，P为该抛物线上一动点，过点P作抛物线对称轴的垂线，垂足为Q，是否存在这样的点P，使以点E，P，Q为顶点的三角形与△AOB相似？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝x+2；（2）y＝x2﹣4x+4；（3）（，），（，），（0，4）或（4，4）．

【解析】

（1）根据点A，B的坐标，利用待定系数法即可求出直线AB的解析式；

（2）设平移后抛物线的解析式为y＝（x﹣m）2（m＞0），则平移后抛物线的对称轴为直线x＝m，点C的坐标为（0，m2），由CD∥x轴，可得出点C，D关于直线x＝m对称，进而可得出点D的坐标，再利用一次函数图象上点的坐标特征即可得出关于m的一元二次方程，解之取其正值即可得出结论；

（3）设点P的坐标为（a，a2﹣4a+4），则PQ＝|a﹣2|，EQ＝a2﹣4a+4，由∠PQE＝90°可得出△EQP∽△AOB或△PQE∽△AOB，①当△EQP∽△AOB时，利用相似三角形的性质可得出关于a的方程，解之即可得出a值，将其代入点P的坐标即可得出结论；②当△PQE∽△AOB时，利用相似三角形的性质可得出关于a的方程，解之即可得出a值，将其代入点P的坐标即可得出结论．综上，此题得解．

解：（1）将A（0，2），B（﹣4，0）代入y＝kx+b，得：

，解得：，

∴直线AB的解析式为y＝x+2．

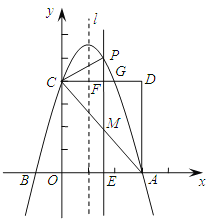
（2）如图1，设平移后抛物线的解析式为y＝（x﹣m）2（m＞0），则平移后抛物线的对称轴为直线x＝m，点C的坐标为（0，m2）．

∵CD∥x轴，

∴点C，D关于直线x＝m对称，

∴点D的坐标为（2m，m2）．

∵点D在直线y＝x+2上，

∴m2＝×2m+2，

解得：m1＝﹣1（舍去），m2＝2，

∴平移后抛物线的解析式为y＝（x﹣2）2，即y＝x2﹣4x+4．

（3）存在这样的点P，使以点E，P，Q为顶点的三角形与△AOB相似．

设点P的坐标为（a，a2﹣4a+4），则PQ＝|a﹣2|，EQ＝a2﹣4a+4．

∵∠PQE＝90°，

∴分两种情况考虑，如图2所示．

①当△EQP∽△AOB时，，即，

化简，得：|a﹣2|＝，

解得：a1＝，a2＝，

∴点P的坐标为（，）或（，）；

②当△PQE∽△AOB时，，即，

化简，得：|a﹣2|＝2，

解得：a1＝0，a2＝4，

∴点P的坐标为（0，4）或（4，4）．

综上所述：存在这样的点P，使以点E，P，Q为顶点的三角形与△AOB相似，点P的坐标为（，），（，），（0，4）或（4，4）．