题目内容
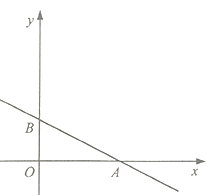
【题目】如图,直线![]() (
(![]() )交
)交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)若点![]() 是直线
是直线![]() 上的任意一点,且点
上的任意一点,且点![]() 与点
与点![]() 距离的最小值为4,求该直线表达式;
距离的最小值为4,求该直线表达式;
(3)在(2)的基础上,若点![]() 在第一象限,且
在第一象限,且![]() 为等腰直角三角形,求点
为等腰直角三角形,求点![]() 的坐标.
的坐标.
【答案】(1)点![]() 的坐标分别是
的坐标分别是![]() ;(2) y=-
;(2) y=-![]() x+2
x+2![]() ;(3)当点
;(3)当点![]() 的坐标是
的坐标是![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰直角三角形.
是等腰直角三角形.
【解析】
(1)利用坐标轴上点的特点即可得出结论;
(2)利用直角三角形的面积相等建立方程求出b=2![]() ,即可得出结论;
,即可得出结论;
(3)①当∠ACB=90°时,先判断出四边形ODCE是矩形,得出OD=CE,CD=OE,∠DCE=90°,再判断出△BCE≌△ACD(AAS),得出BE=AD,CE=CD,进而得出AD=4![]() -m,BE=m-2
-m,BE=m-2![]() ,进而用AD=BE建立方程求解即可得出结论;②③当∠BAC=90°和∠ABC=90°时,构造全等三角形即可得出结论.
,进而用AD=BE建立方程求解即可得出结论;②③当∠BAC=90°和∠ABC=90°时,构造全等三角形即可得出结论.
(1)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() .
.
∴点![]() 的坐标分别是
的坐标分别是![]()
(2)如图,
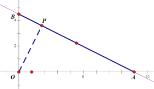
当![]() 时,点
时,点![]() 与点
与点![]() 的距离最小,此时
的距离最小,此时![]() ,
,
∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]()
∵![]()
∴![]()
∴![]() ,
,
∴直线AB的解析式为y=-![]() x+2
x+2![]() ;
;
(3)如图,
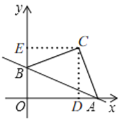
由(1)知,A(4![]() ,0),B(0,2
,0),B(0,2![]() ),
),
∴OA=4![]() ,OB=2
,OB=2![]()
过点C作CD⊥x轴于D,作CE⊥y轴于E,
∵∠DOE=90°,
∴四边形ODCE是矩形,
∴OD=CE,CD=OE,∠DCE=90°,
∴∠BCE+∠BCD=90°,
∵△ABC是等腰直角三角形,
当∠ACB=90°时,
∴BC=AC,∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠BCE=∠ACE,
∴△BCE≌△ACD(AAS),
∴BE=AD,CE=CD,
∴设点C坐标为(m,m),
∴AD=OA-OD=4![]() -m,BE=OE-OB=m-2
-m,BE=OE-OB=m-2![]() ,
,
∴4![]() -m=m-2
-m=m-2![]() ,
,
∴m=3![]() ,
,
∴C(3![]() ,3
,3![]() ),
),
如图2,
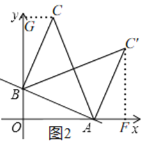
②当∠BAC=90°时,过点C'作C'F⊥x轴于F,
∴∠C'AF+∠AC'F=90°,
∵∠C'AF+∠OAB=90°,
∴∠OAB=∠FC'A,
∵AB=AC',
∴△AOB≌△C'FA(AAS),
∴C'F=OA=4![]() ,AF=OB=2
,AF=OB=2![]() ,
,
∴OF=OA+AF=6![]() ,
,
∴C'(6![]() ,4
,4![]() ),
),
③当∠ABC=90°时,同②的方法得,C(2![]() ,6
,6![]() ),
),
即:点C的坐标为(3![]() ,3
,3![]() )或(6
)或(6![]() ,4
,4![]() )或(2
)或(2![]() ,6
,6![]() ).
).

 习题精选系列答案
习题精选系列答案