题目内容
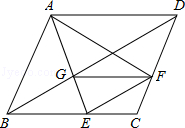
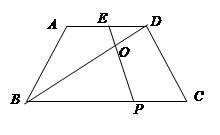
己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
(1)求证:BE=DF;
(2)当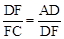 时,求证:四边形BEFG是平行四边形.
时,求证:四边形BEFG是平行四边形.

(1)求证:BE=DF;
(2)当
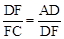 时,求证:四边形BEFG是平行四边形.
时,求证:四边形BEFG是平行四边形.证明:(1)∵四边形ABCD是菱形,∴AB=AD,∠ABC=∠ADF,
∵∠BAF=∠DAE,∴∠BAF﹣∠EAF=∠DAE﹣∠EAF,即:∠BAE=∠DAF。
∴△BAE≌△DAF(ASA)。∴BE=DF。
(2)∵四边形ABCD是菱形,∴AD∥BC。∴△ADG∽△EBG。∴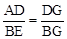 。
。
又∵BE="DF" ,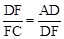 ,∴
,∴ 。∴GF∥BC。
。∴GF∥BC。
∴∠DGF=∠DBC=∠BDC。∴DF=GF。
又∵BE="DF" ,∴BE=GF。∴四边形BEFG是平行四边形。
∵∠BAF=∠DAE,∴∠BAF﹣∠EAF=∠DAE﹣∠EAF,即:∠BAE=∠DAF。
∴△BAE≌△DAF(ASA)。∴BE=DF。
(2)∵四边形ABCD是菱形,∴AD∥BC。∴△ADG∽△EBG。∴
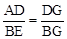 。
。又∵BE="DF" ,
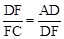 ,∴
,∴ 。∴GF∥BC。
。∴GF∥BC。∴∠DGF=∠DBC=∠BDC。∴DF=GF。
又∵BE="DF" ,∴BE=GF。∴四边形BEFG是平行四边形。
(1)由菱形的性质和∠BAF=∠DAE,证得△ABF与△AFD全等后即可证得结论。(2)由AD∥BC证得△ADG∽△EBG,从而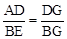 ;由
;由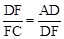 和BE=DF即可得证得
和BE=DF即可得证得 。从而根据平行线分线段成比例定理证得FG∥BC,进而得到∠DGF=∠DBC=∠BDC,根据等腰三角形等角对等边的判定和BE="DF" ,证得BE=GF。利用一组对边平行且相等即可判定平行四边形。
。从而根据平行线分线段成比例定理证得FG∥BC,进而得到∠DGF=∠DBC=∠BDC,根据等腰三角形等角对等边的判定和BE="DF" ,证得BE=GF。利用一组对边平行且相等即可判定平行四边形。
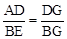 ;由
;由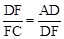 和BE=DF即可得证得
和BE=DF即可得证得 。从而根据平行线分线段成比例定理证得FG∥BC,进而得到∠DGF=∠DBC=∠BDC,根据等腰三角形等角对等边的判定和BE="DF" ,证得BE=GF。利用一组对边平行且相等即可判定平行四边形。
。从而根据平行线分线段成比例定理证得FG∥BC,进而得到∠DGF=∠DBC=∠BDC,根据等腰三角形等角对等边的判定和BE="DF" ,证得BE=GF。利用一组对边平行且相等即可判定平行四边形。
练习册系列答案
相关题目
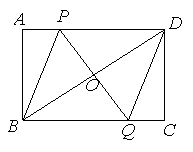
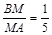 时,求直线PQ的解析式;
时,求直线PQ的解析式;


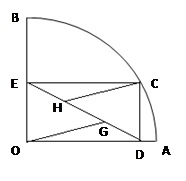
 (1)求证:OG=CH;
(1)求证:OG=CH;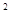
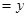 ,CD
,CD ,求
,求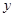 与
与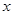 之间的函数关系式.
之间的函数关系式.