题目内容
如图,在直角坐标平面中,O为原点,A(0,6),B(8,0)。点P从点A出发,以每秒2个单位长度的速度沿射线AO方向运动,点Q从点B出发,以每秒一个单位长度的速度沿x轴正方向运动,P,Q两动点同时出发,设移动时间为t(t>0)秒.
(1)在点P,Q的运动过程中,当点P在AO的延长线上时,若△POQ与△AOB相似,求t的值;
(2)如图2,当直线PQ与线段AB交于点M,且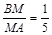 时,求直线PQ的解析式;
时,求直线PQ的解析式;
(3)以点O为圆心,OP长为半径画圆⊙O,以点B为圆心,BQ长为半径画⊙B,讨论⊙O和⊙B的位置关系,并直接写出相应t的取值范围.
(1)在点P,Q的运动过程中,当点P在AO的延长线上时,若△POQ与△AOB相似,求t的值;
(2)如图2,当直线PQ与线段AB交于点M,且
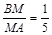 时,求直线PQ的解析式;
时,求直线PQ的解析式;(3)以点O为圆心,OP长为半径画圆⊙O,以点B为圆心,BQ长为半径画⊙B,讨论⊙O和⊙B的位置关系,并直接写出相应t的取值范围.

(1)据题意,t秒时AP=2t,BQ= t,OP =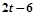 ,OQ=" 8+t" 。
,OQ=" 8+t" 。
若△POQ∽△AOB,则 ,即
,即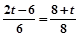 ,
,
解得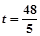 ,
,
若△POQ∽△BOA,则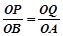 ,即
,即
解得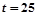 ,
,
∴当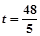 或25时 △POQ与△AOB相似.
或25时 △POQ与△AOB相似.
(2)过M分别作x轴、y轴的垂线,垂足分别为N、G.
根据题意得PO//MN,∴△BMN∽△BAO ∴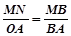
∵ ∴
∴  ∴
∴  ∴ MN=1
∴ MN=1
同理 MG=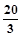 ∴ M(
∴ M(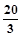 ,1)
,1)
∵ OQ=" 8+t" ∴ NQ=
由△QMN∽△QPO得: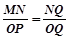 ,即
,即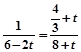 。
。
解得: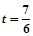 ,或者t=0(舍去)
,或者t=0(舍去)
∴ P(0,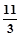 )
)
∴PQ直线解析式: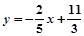
(3)当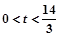 且t≠3时,两圆外离;当
且t≠3时,两圆外离;当 时,两圆外切;当
时,两圆外切;当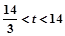 时,两圆相交;当
时,两圆相交;当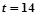 时,两圆内切;当
时,两圆内切;当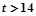 时 两圆内含.
时 两圆内含.
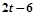 ,OQ=" 8+t" 。
,OQ=" 8+t" 。若△POQ∽△AOB,则
 ,即
,即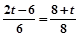 ,
,解得
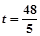 ,
, 若△POQ∽△BOA,则
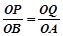 ,即
,即
解得
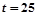 ,
, ∴当
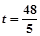 或25时 △POQ与△AOB相似.
或25时 △POQ与△AOB相似. (2)过M分别作x轴、y轴的垂线,垂足分别为N、G.
根据题意得PO//MN,∴△BMN∽△BAO ∴
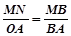
∵
 ∴
∴  ∴
∴  ∴ MN=1
∴ MN=1同理 MG=
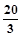 ∴ M(
∴ M(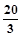 ,1)
,1) ∵ OQ=" 8+t" ∴ NQ=

由△QMN∽△QPO得:
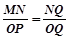 ,即
,即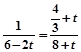 。
。解得:
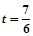 ,或者t=0(舍去)
,或者t=0(舍去)∴ P(0,
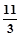 )
) ∴PQ直线解析式:
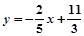
(3)当
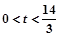 且t≠3时,两圆外离;当
且t≠3时,两圆外离;当 时,两圆外切;当
时,两圆外切;当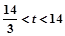 时,两圆相交;当
时,两圆相交;当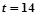 时,两圆内切;当
时,两圆内切;当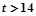 时 两圆内含.
时 两圆内含.(1) △POQ∽△AOB,分两种情况进行讨论;
(2)过M分别作x轴、y轴的垂线,垂足分别为N、G.利用△BMN∽△BAO得出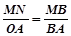 ,从而得出MN的长,同理可得MG的长,得出M点的坐标,同理求出P点坐标,然后再求出PQ的解析式;
,从而得出MN的长,同理可得MG的长,得出M点的坐标,同理求出P点坐标,然后再求出PQ的解析式;
(3)对t进行分段讨论。
(2)过M分别作x轴、y轴的垂线,垂足分别为N、G.利用△BMN∽△BAO得出
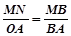 ,从而得出MN的长,同理可得MG的长,得出M点的坐标,同理求出P点坐标,然后再求出PQ的解析式;
,从而得出MN的长,同理可得MG的长,得出M点的坐标,同理求出P点坐标,然后再求出PQ的解析式;(3)对t进行分段讨论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 ( )
( )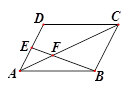

 (D)
(D)
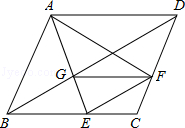
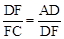 时,求证:四边形BEFG是平行四边形.
时,求证:四边形BEFG是平行四边形.