题目内容
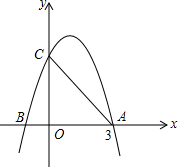 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上是否存在一点P(x,y)(其中x>0,y>0),使△ACP的面积最大?若存在,求出P点的坐标.
考点:二次函数综合题
专题:
分析:(1)把A(3,0)代入y=-x2+2x+m,求解即可,
(2)令0=-x2+2x+3,解得x的值,即可求出点B的坐标,
(3)当直线平行于直线CA,且与抛物线只有一个交点时,△ACP的面积最大,列出点P经过的直线y=-x+b,结合抛物线利用△求出b,再联立即可得出点P的坐标.
(2)令0=-x2+2x+3,解得x的值,即可求出点B的坐标,
(3)当直线平行于直线CA,且与抛物线只有一个交点时,△ACP的面积最大,列出点P经过的直线y=-x+b,结合抛物线利用△求出b,再联立即可得出点P的坐标.
解答:解:(1)∵二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),
∴把A(3,0)代入y=-x2+2x+m,解得m=3,
(2)∵二次函数解析式为y=-x2+2x+3,
∴令0=-x2+2x+3,解得x1=-1,x2=3,
∴点B的坐标为(-1,0),
(3)存在
理由如下:
当直线平行于直线CA,且与抛物线只有一个交点时,△ACP的面积最大,
∵直线CA的解析式为:y=-x+3,
∴设点P经过的直线为y=-x+b,
∴-x+b=-x2+2x+3,化简得x2-3x+b-3=0,△=9-4(b-3)=0,解得b=
,
联立得
,解得
,
∴P点的坐标为(
,
).
∴把A(3,0)代入y=-x2+2x+m,解得m=3,
(2)∵二次函数解析式为y=-x2+2x+3,
∴令0=-x2+2x+3,解得x1=-1,x2=3,
∴点B的坐标为(-1,0),
(3)存在
理由如下:
当直线平行于直线CA,且与抛物线只有一个交点时,△ACP的面积最大,
∵直线CA的解析式为:y=-x+3,
∴设点P经过的直线为y=-x+b,
∴-x+b=-x2+2x+3,化简得x2-3x+b-3=0,△=9-4(b-3)=0,解得b=
| 21 |
| 4 |
联立得
|
|
∴P点的坐标为(
| 3 |
| 2 |
| 15 |
| 4 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是利用△求出b的值.

练习册系列答案
相关题目
以下说法正确的是( )
| A、非负数的绝对值等于本身的数 |
| B、非正数的相反数等于本身的数 |
| C、倒数等于本身的数有±1,0 |
| D、两个负数,绝对值大的仍然大 |
 如图,点A的坐标为(-2,0),点B的坐标为(8,0),以AB为直径作⊙O′,交y轴的负半轴于点C,则点C的坐标为
如图,点A的坐标为(-2,0),点B的坐标为(8,0),以AB为直径作⊙O′,交y轴的负半轴于点C,则点C的坐标为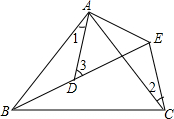 如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=