Question

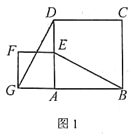
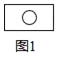
【题目】如图1，点为正方形的中心。

（1）将线段绕点逆时针方向旋转，点的对应点为点，连接， ， ，请依题意补全图1；

（2）根据图1中补全的图形，猜想并证明与的关系；

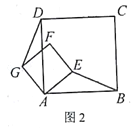
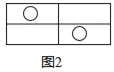
（3）如图2，点是中点，△是等腰直角三角形， 是的中点， ， ， ，△绕点逆时针方向旋转角度，请直接写出旋转过程中的最大值。

Answer 1

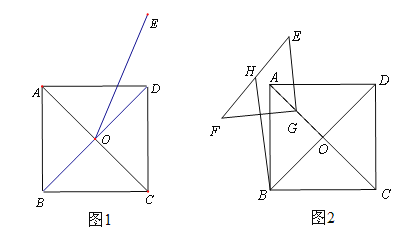
【答案】（1）图形见解析（2）证明见解析（3）

【解析】（1）根据题意画出图形即可；

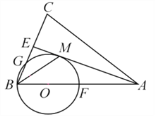
（2）延长EA交OF于点H，交BF于点G，利用正方形的性质和旋转的性质证明△EOA≌△FOB，得到AE=BF．根据等边对等角得到∠OEA=∠OFB，由∠OEA+∠OHA=90°，所以∠OFB+∠FHG=90°，进而得到AE⊥BF．

（3）BH的最大值为.

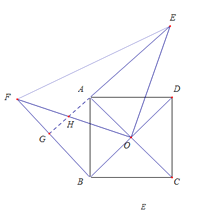
解：（1）正确画出图形，如下图所示：

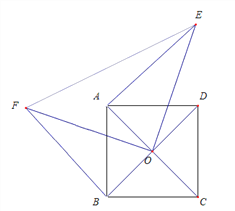
（2）延长EA交OF于点，交于点

∵为正方形的中心，

∴，∠＝90，

∵绕点逆时针旋转90角得到，

∴，

∴∠＝∠＝90，

∴∠＝∠，

在△和△中，

，

∴△≌△，

∴，

∴∠＝∠，

∵∠+∠，

∴∠+∠=90，

∴⊥;

（3）的最大值为.