Question

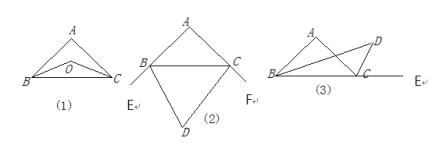
【题目】（1）如图⑴，在△ABC中，∠ABC 、∠ACB的平分线相交于点O，试说明∠BOC＝90°＋∠A；

（2）如图⑵，在△ABC中，BD、CD分别是∠ABC 、∠ACB的外角平分线，试说明∠D＝90°－∠A；

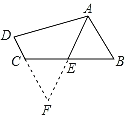
（3）如图⑶，已知BD为△ABC的角平分线，CD为△ABC外角∠ACE的平分线，且与BD交于点D，试说明∠A＝2∠D。

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）证明见解析.

【解析】

（1）根据三角形角平分线的性质可得，∠OBC+∠OCB=90°-∠A，根据三角形内角和定理可得∠BOC=90°+∠A；

（2）根据三角形外角平分线的性质可得∠BCD=（∠A+∠ABC）、∠DBC=（∠A+∠ACB）；根据三角形内角和定理可得∠BDC=90°-∠A；

（3）根据BD为△ABC的角平分线，CD为△ABC外角∠ACE的平分线，可知，∠A=180°-∠1-∠3，∠D=180°-∠4=∠5=180°-∠3-（∠A+2∠1），两式联立可得2∠D=∠A．

（1）证明：∵在△ABC中，OB、OC分别是∠ABC、∠ACB的平分线，

∴∠OBC+∠OCB=（180°-∠A）=90°-∠A，

故∠BOC=180°-（∠OBC+∠OCB）=180°-（90°-∠A）=90°+∠A；

（2）证明：∵BD、CD分别是∠ABC 、∠ACB的外角平分线，

∴∠BCD=（∠A+∠ABC）、∠DBC=（∠A+∠ACB），

由三角形内角和定理得，∠BDC=180°-∠BCD-∠DBC，

=180°- [∠A+（∠A+∠ABC+∠ACB）]，

=180°-（∠A+180°），

=90°-∠A；

（3）证明：如图：

∵BD为△ABC的角平分线，交AC与点E，CD为△ABC外角∠ACE的平分线，两角平分线交于点D，

∴∠1=∠2，∠5=（∠A+2∠1），∠3=∠4，

在△ABE中，∠A=180°-∠1-∠3，

∴∠1+∠3=180°-∠A①，

在△CDE中，∠D=180°-∠4-∠5=180°-∠3-（∠A+2∠1），

即2∠D=360°-2∠3-∠A-2∠1=360°-2（∠1+∠3）-∠A②，

把①代入②得2∠D=∠A．