题目内容
【题目】在![]() 中,对角线AC、BD交于点O,且分别平分∠DAB,∠ABC.
中,对角线AC、BD交于点O,且分别平分∠DAB,∠ABC.
(1)请求出∠AOB的度数,写出AD、AB、BC之间的等量关系,并给予证明.
(2)设点P为对角线AC上一点,PB=5,若AD+BC=16,四边形ABCD的面积为![]() ,求AP的长.
,求AP的长.
【答案】(1)![]() ,
,![]() ;证明见解析;(2)
;证明见解析;(2)![]() 的长为
的长为![]() .
.
【解析】
(1)根据平行四边形的性质可得![]() ,由AC、BD分别平分∠DAB、∠ABC可得
,由AC、BD分别平分∠DAB、∠ABC可得![]() ,根据三角形内角和定理即可得∠AOB的度数;根据平行线的性质可得
,根据三角形内角和定理即可得∠AOB的度数;根据平行线的性质可得![]() ,即可证明
,即可证明![]() ,可得AB=BC,根据平行四边形的性质可得
,可得AB=BC,根据平行四边形的性质可得![]() ;
;
(2)根据AD+BC=16可得![]() =8,当∠ABC>90°时,过点
=8,当∠ABC>90°时,过点![]() 作
作![]() ,根据四边形ABCD的面积可得DE的长,利用勾股定理可求出AE的长,进而可证明△DAB是等边三角形,根据含30°角的直角三角形的性质可得OA、OB的长,根据PB=5,利用勾股定理可得OP的长,即可求出AP的长;当∠ABC<90°时,可得OB>5,不符合题意,综上即可得答案.
,根据四边形ABCD的面积可得DE的长,利用勾股定理可求出AE的长,进而可证明△DAB是等边三角形,根据含30°角的直角三角形的性质可得OA、OB的长,根据PB=5,利用勾股定理可得OP的长,即可求出AP的长;当∠ABC<90°时,可得OB>5,不符合题意,综上即可得答案.
(1)∵四边形ABCD为平行四边形,
∴![]() ,
,
∴![]() ,
,
∵AC、BD分别平分∠DAB、∠ABC,
∴![]() ,
,
∴![]() ,
,
![]() 之间的等量关系为
之间的等量关系为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵AC平分![]() ,
,
![]()
![]() ,
,
![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]()
![]()
(2)∵![]() ,
,
∴![]() ,
,
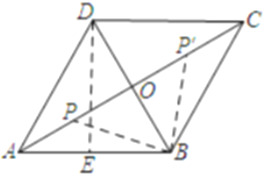
①如图,当![]() 时,
时,
过点![]() 作
作![]() ,
,
∵四边形![]() 的面积为
的面积为![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 为
为![]() 的中点,
的中点,![]() ,
,
![]()
![]() 为等边三角形,
为等边三角形,
![]()
![]()
∵∠AOB=90°,
![]() ,
,
∵![]() ,
,
![]()
![]() 或
或![]() .
.
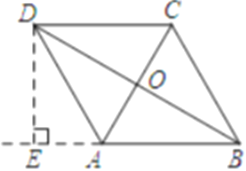
②如图,当![]() 时,
时,
![]() ,AE=4,
,AE=4,
∴BE=12,
∴BD=![]() =
=![]() ,
,
∴![]() ,
,
所以这样的点![]() 不存在,故排除.
不存在,故排除.
综上所述:![]() 的长为
的长为![]() .
.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目






