题目内容
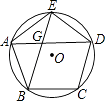
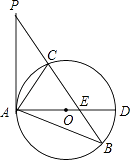
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
【答案】
(1)证明:∵BE平分∠BAC,AD平分∠ABC,
∴∠ABE=∠CBE,∠BAE=∠CAD,
∴ ![]() ,
,
∴∠DBC=∠CAD,
∴∠DBC=∠BAE,
∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
∴∠DBE=∠DEB,
∴DE=DB
(2)解:连接CD,如图所示:
由(1)得: ![]() ,
,
∴CD=BD=4,
∵∠BAC=90°,
∴BC是直径,
∴∠BDC=90°,
∴BC= ![]() =4
=4 ![]() ,
,
∴△ABC外接圆的半径= ![]() ×4
×4 ![]() =2
=2 ![]() .
.
【解析】(1)由角平分线得出∠ABE=∠CBE,∠BAE=∠CAD,得出 ![]() ,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;(2)由(1)得:
,由圆周角定理得出∠DBC=∠CAD,证出∠DBC=∠BAE,再由三角形的外角性质得出∠DBE=∠DEB,即可得出DE=DB;(2)由(1)得: ![]() ,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC=
,得出CD=BD=4,由圆周角定理得出BC是直径,∠BDC=90°,由勾股定理求出BC= ![]() =4
=4 ![]() ,即可得出△ABC外接圆的半径.
,即可得出△ABC外接圆的半径.

练习册系列答案
相关题目