Question

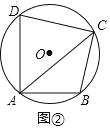
【题目】(1)观察发现;如图1,在中，，点在边上，过作交于，.填空:

①与是否相似? (直接回答)______；

②_______; .

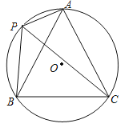
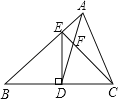
(2)拓展探究:将绕顶点旋转到图2所示的位置，猜想与是否相似?若不相似，说明理由;若相似，请证明.

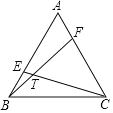
(3)迁移应用:将绕顶点旋转到点在同一条直线上时，直接写出线段的长是 .

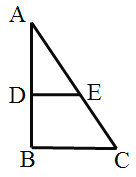
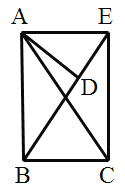
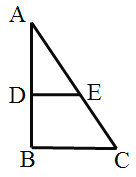
图1 图2 图3

Answer 1

【答案】(1) ①，见解析；②，； (2) ，见解析；(3) 线段的长为或

【解析】

（1）①与有公共角以及，即可知.

②由结合勾股定理得到DE，利用求得AC的值.

（2）猜想，利用，建立相似比进而得到从而证得猜想.

（3）首先由题意可知将绕顶点旋转到点在同一条直线上时有两种情况，对两种情况依次讨论即可.

解：(1)①相似(或)

，

②；

；

，

，

，

，

，即，

解得，，

(2)，

证明：如图2，由旋转变换的性质可知，，

由(1)得，

，

，

；

(3)线段的长为或．

将绕顶点旋转到点在同一条直线上时有两种情况：

①如图2，在中，

点在同一条直线上，

，

②如图3，．