Question

【题目】已知四边形ABCD内接于⊙O，∠DAB＝90°

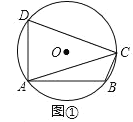
（1）如图①，若∠ACB＝60°，AB＝4，求⊙O的直径；

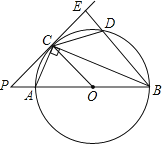
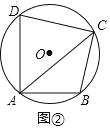
（2）如图②，若AD≠AB，点C为弧DB的中点且AD＝m，AB＝n，求AC的长．

Answer 1

【答案】（1）8；（2）m+n

【解析】

（1）由圆周角定理可得∠ACB＝∠ADB＝60°，由三角函数可求BD的长，即可求⊙O的直径；

（2）由题意可得DB＝CD，通过证明△DEC∽△DAB，可得，可得DE＝m，EC＝n，即可求得AC＝AE+EC＝m+n．

解：（1）如图，连接BD，

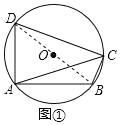
∵∠DAB＝90°

∴BD是直径，

∵∠DAB＝90°，∠ACB＝∠ADB＝60°，AB＝4，

∴sin∠ADB＝

∴DB＝＝8

∴⊙O的直径为8

（2）如图，连接BD，过点D作DE⊥AC于点E，

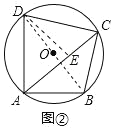
∵∠DAB＝90°

∴BD是直径，

∴∠BCD＝90°

∵点C为弧DB的中点

∴∠DAC＝∠CAB＝45°

∴CD＝BC，

∴DB＝CD

∵∠DCA＝∠ABD，∠DEC＝∠DAB＝90°

∴△DEC∽△DAB

∴

∴＝

∴DE＝m，EC＝n，

∵∠DAC＝45°，DE⊥AC

∴AE＝DE＝m

∴AC＝AE+EC＝m+n