Question

19．如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，且∠CDB=∠OBD=30°，⊙O的半径为6cm．
（1）求证：AC是⊙O的切线；
（2）求由弦CD、BD与弧B超所围成的阴影部分的面积（结果保留π）．

Answer 1

分析 （1）连接CO，由角的等量关系可以证得∠ACO=90°，即能证得切线存在，
（2）首先证明△CDE≌△OBE，阴影部分面积等于S_扇形OBC．

解答 （1）证明：连接CO．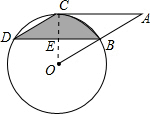
∵∠CDB=∠OBD=30°，
∴∠BOC=60°，
∵AC∥BD，
∴∠A=∠OBD=30°，
∴∠ACO=90°．
∴AC为⊙O切线．

（2）解：∵∠CDB=∠OBD=30°，
又∵∠CED=∠BEO，BE=ED，
∴△CDE≌△OBE．
∴S阴=S扇OBC=$\frac{60π•{6}^{2}}{360}$=6π（cm²），
答：阴影部分的面积为6πcm²．

点评 本题考查了切线的判定，扇形面积的计算和解直角三角形等知识点．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．