题目内容
 在如图所示的平行四边形ABCD中对角线AC.BD交于点O,EF⊥AC,O为垂足,EF分别交AB,CD于点E,F,且BE=OE=
在如图所示的平行四边形ABCD中对角线AC.BD交于点O,EF⊥AC,O为垂足,EF分别交AB,CD于点E,F,且BE=OE=| 1 |
| 2 |
考点:矩形的判定
专题:证明题
分析:首先根据已知得出∠OAE=30°,进而得出AO=BO,即可得出答案.
解答:证明:∵EF⊥AC,
∴∠AOE=90°
∵OE=
AE,
∴∠OAE=30°,
∴∠OEA=60°,∠0BE=30°,
∴OA=OB,
∴AC=BD
∴平行四边形ABCD是矩形.
∴∠AOE=90°
∵OE=
| 1 |
| 2 |
∴∠OAE=30°,
∴∠OEA=60°,∠0BE=30°,
∴OA=OB,
∴AC=BD
∴平行四边形ABCD是矩形.
点评:此题主要考查了矩形的判定以及直角三角形的性质,得出∠OAE=30°是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
现要做一个直角三角形的木架,以下四组木棒中,符合条件的是( )
| A、10cm,6cm,4cm |
| B、8cm,12cm,15cm |
| C、12cm,15cm,17cm |
| D、15cm,17cm,8cm |
计算(-
)-3的正确结果是( )
| 1 |
| a |
| A、a3 | ||
| B、-a3 | ||
C、
| ||
D、-
|
下列各组整式中,是同类项的一组是( )
| A、2t与t2 |
| B、2t与t+2 |
| C、t2与t+2 |
| D、2t与t |
下列各组中的两项,不是同类项的是( )
| A、a2b与ab2 |
| B、-x2y与2yx2 |
| C、2πr与2r |
| D、35与53 |
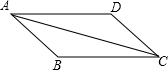 如图,△ABC≌△CDA,下列结论:①AB=CD,BC=DA;②∠BAC=∠DCA,∠ACB=∠CAD;③AB∥CD,BC∥DA,其中正确的个数是( )
如图,△ABC≌△CDA,下列结论:①AB=CD,BC=DA;②∠BAC=∠DCA,∠ACB=∠CAD;③AB∥CD,BC∥DA,其中正确的个数是( )