题目内容
如图2 - 50所示,抛物线y=-(x+1)2+m(x+1)(m为常数)与x轴交于A,B两点,与y轴交于点C,顶点M在第一象限,△AOC的面积为1.5,点D是线段AM上一个动点,在矩形DEFG中,点G,F在x轴上,点E在MB上.
(1)求抛物线的解析式;
(2)当DE=1时,求矩形DEFG的面积;
(3)矩形DEFG的面积是否存在最大值?如果存在,请求出这个最大值,并指出此时点D的坐标;如果不存在,请说明理由.
解:(1)由y=-(x+1)2+m(x+1),得A(-1,0),C(0,m-1),则OA=l,OC =m-1.∵S△OAC=1.5,∴
=m-1.∵S△OAC=1.5,∴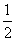 ×1×(m-1
×1×(m-1 )=1.5,∴m=4,∴y=-x2+2x+3.(2)由y=-(x-1)2+4,令y=0,得-(x-1)2+4=0,解得x1=-1,x2=3,∴A(-l,0),B(3,0),M(1,4),∴直线AM的解析式为y=2x+2.由点D在线段AM上,可设点D的坐标为(a,2a+2),-1<a<1.当DE=1时,由抛物线对称性可知1-a=0.5,∴a=0.5,2a+2=3,∴S矩形DEFG=DE·DG=1×3=3. (3)S矩形DEFG存在最大值.设D点坐标为(a,2a+2),-l<a<l,由抛物线对称性可知D
)=1.5,∴m=4,∴y=-x2+2x+3.(2)由y=-(x-1)2+4,令y=0,得-(x-1)2+4=0,解得x1=-1,x2=3,∴A(-l,0),B(3,0),M(1,4),∴直线AM的解析式为y=2x+2.由点D在线段AM上,可设点D的坐标为(a,2a+2),-1<a<1.当DE=1时,由抛物线对称性可知1-a=0.5,∴a=0.5,2a+2=3,∴S矩形DEFG=DE·DG=1×3=3. (3)S矩形DEFG存在最大值.设D点坐标为(a,2a+2),-l<a<l,由抛物线对称性可知D E=2(1-a),DG=2a+2.∴S矩形DEFG=DE·DG=2(1-a)·(2a+2)=-4a2+4,而-1<a<l,∴当a=0时,S取得最大值为4,此时D点坐标为(0,2).
E=2(1-a),DG=2a+2.∴S矩形DEFG=DE·DG=2(1-a)·(2a+2)=-4a2+4,而-1<a<l,∴当a=0时,S取得最大值为4,此时D点坐标为(0,2).

练习册系列答案
相关题目
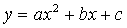 图象如图所示,则下列结论正确的( )
图象如图所示,则下列结论正确的( )
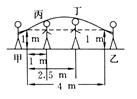
 图2 - 78所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为 ( )
图2 - 78所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为 ( )