题目内容
19.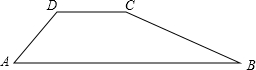 如图,某一大坝的横截面是四边形ABCD.其中AB∥DC,坝顶宽CD=3m,坝高6m,迎水坡BC的坡度i1=1:2.背水坡AD的坡度i2=1:1,求斜坡AD坡角∠A和坝底宽AB.
如图,某一大坝的横截面是四边形ABCD.其中AB∥DC,坝顶宽CD=3m,坝高6m,迎水坡BC的坡度i1=1:2.背水坡AD的坡度i2=1:1,求斜坡AD坡角∠A和坝底宽AB.
分析 过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,得到两个直角三角形和一个矩形,在Rt△AED中利用DE和AD的长,求得线段AE的长和∠A的度数;在Rt△BCF中利用BC的坡度和CF的长求得线段BF的长,然后与AE、EF相加即可求得AB的长.
解答  解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形,
解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形,
则CD=FE=3m,CF=ED=6m,
∵背水坡AD的坡度i2=1:1,
∴AE=DE=6m,
在Rt△AED中,AD=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$m,
∵tan∠A=$\frac{DE}{AE}$=1,
∴∠A=45°,
∵迎水坡BC的坡度i1=1:2,CF=6m,
∴FB=2CF=12米,
则AB=BF+EF+AE=12+3+6=21,
故斜坡AD的坡角∠A为45°,坝底宽AB的长度为21m.
点评 此题主要考查了解直角三角形的应用,解决本题的关键是利用锐角三角函数的概念和坡度的概念求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
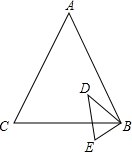 如图,已知在△ABC和△EBD中,$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$.
如图,已知在△ABC和△EBD中,$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$. 如图,已知等腰△ABC中,腰AB=8c,DE是腰AC的垂直平分线,垂足为点D,与AB相交于点E,△BCE的周长为14cm,求BC的长.
如图,已知等腰△ABC中,腰AB=8c,DE是腰AC的垂直平分线,垂足为点D,与AB相交于点E,△BCE的周长为14cm,求BC的长.