题目内容
 两个等腰直角三角形ACB和DCE的位置如图所示,点A、C、E和点B、C、D分别在一直线上,∠ACB=90°,
两个等腰直角三角形ACB和DCE的位置如图所示,点A、C、E和点B、C、D分别在一直线上,∠ACB=90°, ,AB=3DE,点G、H分别是△ACB、△DCE的重心,联结GH,那么GH=________.
,AB=3DE,点G、H分别是△ACB、△DCE的重心,联结GH,那么GH=________.
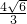
分析:根据等腰直角三角形的性质求出两个三角形△CDE和△ABC的斜边上的高的和,再根据三角形的重心到顶点的距离等于到底边的对边中点的2倍计算即可得解.
解答:∵AE=4
 ,△ACB、△CDE是等腰直角三角形,
,△ACB、△CDE是等腰直角三角形,∴△CDE和△ABC的斜边上的高的和=
 ×4
×4 =2
=2 ,
,∵点G、H分别是△ACB、△DCE的重心,
∴GH=
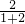 ×2
×2 =
=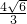 .
.故答案为:
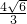 .
.点评:本题考查了三角形的重心,三角形的重心到顶点的长度等于到对边中点的长度的2倍,等腰直角三角形的性质.

练习册系列答案
相关题目
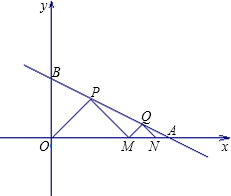 ∠OPM=∠MQN=90°.试求:
∠OPM=∠MQN=90°.试求: