Question

如图，在△ABC中，∠ABC=90°，D为AB延长线上一点，点E在BC边上且BE=BD，连结AE、DE、DC，AE=DC．

（1）求证：AB=BC，AE⊥DC；

（2）若∠CAE=30°，求∠BDC的度数．

Answer 1

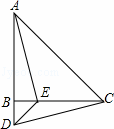
（1）证明：在△ABE和△CBD中，延长AE与DC相交于点F，如图：

在RT△ABE与RT△CBD中，

，

∴RT△ABE≌RT△CBD（HL），

∴AB=BC；

∵△ABE≌△CBD，

∴∠BAE=∠BCD，

∵∠BAE+∠AEB=90°，

∴∠BCD+∠CEF=90°，

∴∠EFC=90°，

即AF⊥DC

（2）解：∵△ABE≌△CBD，

∴∠AEB=∠BDC，

∵∠AEB为△AEC的外角，

∴∠AEB=∠ACB+∠CAE=30°+45°=75°，

则∠BDC=75°．