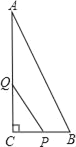
��Ŀ����
����Ŀ����ͼ1������ABC�У���BC����ȡһ��P����AC����ȡһ��D����AP��PD�������APD�ǵ�������������ABP����CDP���ƣ����dz���APD��AC���ϵ���������������������.
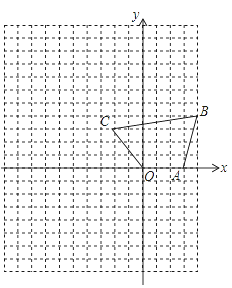
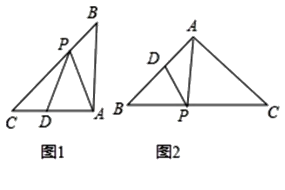
(1)��ͼ2,����ABC��AB=AC,��B=50������APD��AB���ϵ�������������������������AD=DP����PAC=��BPD�����PAC�Ķ�����___��
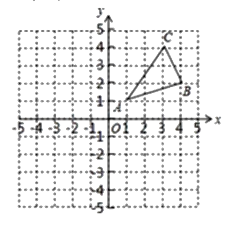
(2)��ͼ3������ABC�У���A=2��C����AC�������ٴ���һ����������������APD�����뻭��һ��AC���ϵ���������������APD������˵�����ɣ�
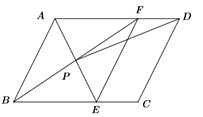
(3)��ͼ4����Rt��ABC��AB=AC=2����APD��AB���ϵ�������������������������д��AD���ȵ����п���ֵ.
���𰸡���1��30������2������������3��AD�ij�Ϊ1��![]() ��
��![]() .
.
��������
��1�����ݵȱ߶ԵȽǺ���������ǵ�����֤����B����PAB���ɽ�����⣮
��2����ͼ3�У�����BAC��ƽ����AP��BC��P����PD��AB��AC��D������ƽ���ߵ����ʺͽ�ƽ���߶���ɵá�BAP=��PAD=��DPA����CPD=��B����ϡ�A=2��C��֤��APD�ǵ�������������APB����CDP���ƣ����ɽ�����⣮
��3���������������ۣ���ͼ3���У���DA��DPʱ����ͼ4�У���PA��PDʱ����ͼ5�У���AP��ADʱ���ֱ���⼴�ɽ�����⣮
�⣺��1����ͼ2�У�
��AB��AC��DA��DP��
���B����C����DAP����DPA��
�ߡ�PAC����BPD��
���APC����BDP����DAP����DPA��
�ߡ�APC����B����BAP��
���B����PAB��50����
�ߡ�BAC��180��50��50����80����
���PAC��30��
�ʴ�Ϊ30����
��2����ͼ3�У���APD��AC���ϵ�����������������������
���ɣ�����BAC��ƽ����AP��BC��P����PD��AB��AC��D��
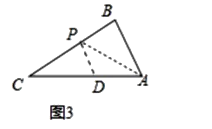
���BAP=��PAD=��DPA����CPD=��B��
��DP=DA��
�ߡ�CAB=2��C��
���BAP =��C��
���APD�ǵ����������ҡ�APB���CDP���ƣ�
���APD��AC���ϵ�����������������������
��3����ͼ3���У���DA=DPʱ�����APD=��DAP=x��
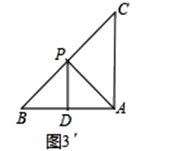
������BPD=��CAP=90��-x����BDP=��CPA=2x��
��90��-x+2x+x=180����
��x=45����
�������ζ��ǵ���ֱ�������Σ���֪AD=1��
������PDB=��CAPʱ�����APD=��DAP=x��
�õ���PDB=��CAP=2x����֪x=30����
��AD=a����AP=![]()
�ߡ�BPD�ס�CPA��
��![]() ����
����![]() ��
��
���![]() ��
��
��ͼ4�У���PA=PDʱ����֪��PDB�Ƕ۽ǣ���CAP����ǣ�
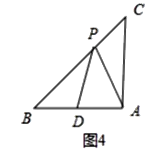
���PDB=��CPA�����BPD�ա�CPA��
��AD=a����BD=2-a��![]() ��AC=2��
��AC=2��
![]() ��
��
���a=![]() ��
��
��ͼ5�У���AP=ADʱ�����APD=��ADP=x�����DAP=180��-2x����֪��PDBΪ�۽ǣ���CAPΪ��ǣ�
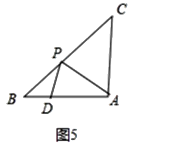
���PDB=��CPA=180��-x����CAP=90��-��DAP=90��-��180��-2x��=2x-90����
�ڡ�APC�У�2x-90��+180��-x+45��=180����
���x=45���������ܳ�����
����������AD�ij�Ϊ1��![]() ��
��![]() .
.