题目内容
如图点A点B是反比例函数上两点,过这两点的直线 ,且AC∥X轴,AC⊥BC于点C,
①求阴影部分面积(用k的代数式表示);
 ②若BC和AC分别交x轴、y轴于D,E,连接DE,求证△ABC~
△EDC;
②若BC和AC分别交x轴、y轴于D,E,连接DE,求证△ABC~
△EDC;
③若 求出这两个函数解析式。

【答案】
①  , ②
, ② 
 ,
,

∴DE边上的高相等,∴DE∥AB 。∴△ABC∽△EDC;
。∴△ABC∽△EDC;
③ 反比例函数: ;一次函数:
;一次函数: 。
。
【解析】①先由点A点B的坐标求出△ABC的面积,再由直线AB与坐标轴的交点坐标求出直线AB与坐标轴围成的面积,即可表示出阴影部分面积;
②先得到DE边上的高相等,则DE∥AB,所以△ABC∽△EDC。
③由△ABC的面积可求得k的值,即可求出这两个函数解析式。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 两个反比例函数y=
两个反比例函数y=| k |
| x |
| 1 |
| x |
| k |
| x |
| 1 |
| x |
| 1 |
| x |
| k |
| x |
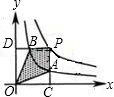
| A、△ODB与△OCA的面积相等 |
| B、四边形PAOB的面积不会发生变化 |
| C、PA与PB始终相等 |
| D、当点A是PC的中点时,点B一定是PD的中点 |
 如图,若点P是反比例函数y=
如图,若点P是反比例函数y= ②若BC和AC分别交x轴、y轴于D,E,连接DE,求证△ABC~ △EDC;
②若BC和AC分别交x轴、y轴于D,E,连接DE,求证△ABC~ △EDC;
