题目内容
3.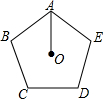 如图,点O是正五边形ABCDE的中心,则∠BAO的度数为54°.
如图,点O是正五边形ABCDE的中心,则∠BAO的度数为54°.
分析 连接OB,则OB=OA,得出∠BAO=∠ABO,再求出正五边形ABCDE的中心角∠AOB的度数,由等腰三角形的性质和内角和定理即可得出结果.
解答 解:连接OB,
则OB=OA,
∴∠BAO=∠ABO,
∵点O是正五边形ABCDE的中心,
∴∠AOB=$\frac{360°}{5}$=72°,
∴∠BAO=$\frac{1}{2}$(180°-72°)=54°;
故答案为:54°.
点评 本题考查了正五边形的性质、等腰三角形的性质、正五边形中心角的求法;熟练掌握正五边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.点A(-5,y1)和B(-2,y2)都在直线y=-3x上,则y1与y2的关系是( )
| A. | y1≤y2 | B. | y1=y2 | C. | y1<y2 | D. | y1>y2 |
11.某几何体的三视图如图所示,该几何体是( )
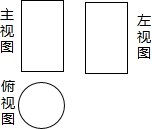

| A. | 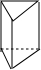 | B. |  | C. |  | D. | 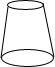 |
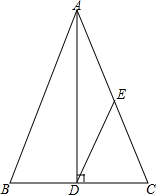 如图,在△ABC中,∠B=∠C,AD⊥BC,垂足为D,DE∥AB交AC于点E.
如图,在△ABC中,∠B=∠C,AD⊥BC,垂足为D,DE∥AB交AC于点E.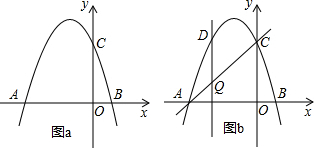
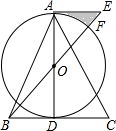 如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.
如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.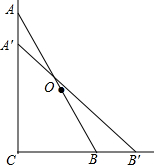 如图,一架梯子AB长2.5m,顶端A靠在墙AC上,此时,梯子下端B与墙角C距离为1.5m,现梯子滑动后停在A′B′的位置上,测得BB′长为0.5m.
如图,一架梯子AB长2.5m,顶端A靠在墙AC上,此时,梯子下端B与墙角C距离为1.5m,现梯子滑动后停在A′B′的位置上,测得BB′长为0.5m.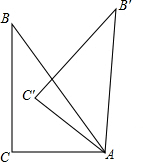 如图,在△ABC中,∠C=90°,∠BAC=60°,AC=2,将△ABC绕点A顺时针旋转α(0°<α<180°),记旋转中△ABC为△A′B′C′,在旋转过程中B′C′所在的直线与线段BC(不含B点)交于点P,与线段AB(不含B点)交于点Q,当BP=BQ时,PQ=2$\sqrt{6}$+4$\sqrt{3}$-2$\sqrt{2}$-8.
如图,在△ABC中,∠C=90°,∠BAC=60°,AC=2,将△ABC绕点A顺时针旋转α(0°<α<180°),记旋转中△ABC为△A′B′C′,在旋转过程中B′C′所在的直线与线段BC(不含B点)交于点P,与线段AB(不含B点)交于点Q,当BP=BQ时,PQ=2$\sqrt{6}$+4$\sqrt{3}$-2$\sqrt{2}$-8.