题目内容
求值:
(1)已知:x=1-
,y=1+
,求(
+
)÷
的值.
(2)已知(x-15)2=169,(y-1)3=-0.125,求
-
-
的值.
(1)已知:x=1-
| 2 |
| 2 |
| 1 |
| x+y |
| 1 |
| x-y |
| 2x |
| x2-2xy+y2 |
(2)已知(x-15)2=169,(y-1)3=-0.125,求
| x |
| 2xy |
| 3 | 2y-x |
考点:分式的化简求值,二次根式的化简求值
专题:
分析:(1)先求得x+y、x-y的值,然后代入化简后的代数式求值.
(2)先求得x、y的值,然后代入求值.
(2)先求得x、y的值,然后代入求值.
解答:解:(1)∵x=1-
,y=1+
,
∴x+y=2,x-y=-2
,
∴原式=
×
=
=
=-
;
(2)∵(x-15)2=169,(y-1)3=-0.125,
∴x-15=±13,y-1=-
解得 x=28或2,y=
,
则
-
-
=
-
-
=2
-2
-
=3,
或
-
-
=
-
-
=
-
+1=1,
即原式=3或1.
| 2 |
| 2 |
∴x+y=2,x-y=-2
| 2 |
∴原式=
| 2x |
| (x+y)(x-y) |
| (x+y)2 |
| 2x |
| x-y |
| x+y |
-2
| ||
| 2 |
| 2 |
(2)∵(x-15)2=169,(y-1)3=-0.125,
∴x-15=±13,y-1=-
| 1 |
| 2 |
解得 x=28或2,y=
| 1 |
| 2 |
则
| x |
| 2xy |
| 3 | 2y-x |
| 28 |
2×28×
|
| 3 | 2×
| ||
| 7 |
| 7 |
| 3 | -27 |
或
| x |
| 2xy |
| 3 | 2y-x |
| 2 |
2×2×
|
| 3 | 2×
| ||
| 2 |
| 2 |
即原式=3或1.
点评:本题考查了分式的化简求值、二次根式的化简求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,三边长满足b2-a2=c2,则互余的一对角是( )
| A、∠A与∠B |
| B、∠C与∠A |
| C、∠B与∠C |
| D、∠A、∠B、∠C |
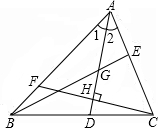 如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上一点,CF⊥AD于H,下面判断正确的有( )
如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上一点,CF⊥AD于H,下面判断正确的有( )