题目内容
已知:过⊙O外的定点P作⊙O的两条切线,分别切⊙O于A、B,在劣弧
上任取一点C,经过点C作⊙O的切线,分别交PA,PB于点D、E.
求证:(1)△PDE的周长是定值(PA+PB);
(2)∠DOE的大小是定值(
∠AOB).
 |
| AB |
求证:(1)△PDE的周长是定值(PA+PB);
(2)∠DOE的大小是定值(
| 1 |
| 2 |
考点:切线长定理
专题:证明题
分析:(1)利用切线长定理得出△PDE的周长=PD+PE+DE=PD+DC+EC+PE=PA+PB,即可得出答案;
(2)利用切线长定理以及三角形内角和定理得出∠AOD=∠DOC,∠COE=∠BOE,进而求出即可.
(2)利用切线长定理以及三角形内角和定理得出∠AOD=∠DOC,∠COE=∠BOE,进而求出即可.
解答: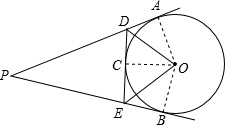 证明:(1)如图:
证明:(1)如图:
∵过⊙O外的定点P作⊙O的两条切线,分别切⊙O于A、B,在劣弧
上任取一点C,经过点C作⊙O的切线,
∴DA=DC,EC=EB,
∴△PDE的周长=PD+PE+DE=PD+DC+EC+PE=PA+PB,
故△PDE的周长是定值(PA+PB);
(2)连接AO,BO,CO,
∵PA,PB,DE为⊙O的切线,
∴∠OAD=∠DCO=∠OBE=90°,∠ADO=∠CDO,∠CEO=∠BEO,
∴∠AOD=∠DOC,∠COE=∠BOE,
∴∠DOE=
∠AOB,
即∠DOE的大小是定值(
∠AOB).
 证明:(1)如图:
证明:(1)如图:∵过⊙O外的定点P作⊙O的两条切线,分别切⊙O于A、B,在劣弧
 |
| AB |
∴DA=DC,EC=EB,
∴△PDE的周长=PD+PE+DE=PD+DC+EC+PE=PA+PB,
故△PDE的周长是定值(PA+PB);
(2)连接AO,BO,CO,
∵PA,PB,DE为⊙O的切线,
∴∠OAD=∠DCO=∠OBE=90°,∠ADO=∠CDO,∠CEO=∠BEO,
∴∠AOD=∠DOC,∠COE=∠BOE,
∴∠DOE=
| 1 |
| 2 |
即∠DOE的大小是定值(
| 1 |
| 2 |
点评:此题主要考查了切线长定理,熟练记忆切线长定理是解题关键.

练习册系列答案
相关题目

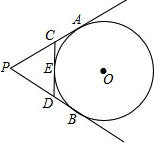 PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是
PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是