题目内容
20.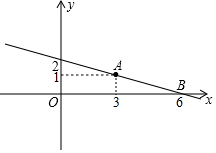 如图,直线y=kx+b经过A(3,1)和B(6,0)两点,则不等式组0<kx+b<$\frac{1}{3}$x的解集为( )
如图,直线y=kx+b经过A(3,1)和B(6,0)两点,则不等式组0<kx+b<$\frac{1}{3}$x的解集为( )| A. | 3<x<6 | B. | x>3 | C. | x<6 | D. | x>3或x<6 |
分析 将A(3,1)和B(6,0)分别代入y=kx+b,求出k、b的值,再解不等式组0<kx+b<$\frac{1}{3}$x的解集.
解答 解:将A(3,1)和B(6,0)分别代入y=kx+b得,$\left\{\begin{array}{l}{3k+b=1}\\{6k+b=0}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=2}\end{array}\right.$,
则函数解析式为y=-$\frac{1}{3}$x+2.
可得不等式组 $\left\{\begin{array}{l}{-\frac{1}{3}x+2>0}\\{-\frac{1}{3}x+2<\frac{1}{3}x}\end{array}\right.$,
解得3<x<6.
故选A.
点评 本题考查了一次函数与一元一次不等式,利用待定系数法求出函数解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.一次函数y=(m+3)x-5的函数值y随x的增大而减小,则m的取值是( )
| A. | m<3 | B. | m>3 | C. | m<-3 | D. | m>-3 |
8.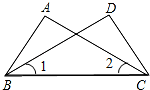 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是( )
 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是( )| A. | AB=CD | B. | AC=BD | C. | ∠A=∠D | D. | ∠ABC=∠DCB |
5.化简(-x)3结果正确的是( )
| A. | x3 | B. | -x3 | C. | -x | D. | x |
10.一组数据1,2,3,5,4,3中的中位数和众数分别是( )
| A. | 3,3 | B. | 5,3 | C. | 4,3 | D. | 5,10 |
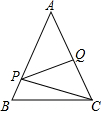 图中,P及Q分别为AB及AC上的点使得PQ为△APC的一条垂直平分线,若QC=6cm及△BCP的周长为21cm,求△ABC的周长.
图中,P及Q分别为AB及AC上的点使得PQ为△APC的一条垂直平分线,若QC=6cm及△BCP的周长为21cm,求△ABC的周长. 如图,已知a∥b,若∠3=120°,则∠1=60°;∠2=60°.
如图,已知a∥b,若∠3=120°,则∠1=60°;∠2=60°.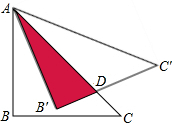 如图,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转一定角度α(α为锐角)后得到△AB′C′.使得B′C′交AC边于点D,点D不与点B′重合,则有下列结论:①∠ADB′=45°+α;②∠α<45°;③若AD的长为整数,则AD等于7cm;④当α=15°时,阴影部分的面积为6$\sqrt{3}$cm2.其中正确结论的序号是①②④(把所有正确的序号都填在横线上)
如图,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转一定角度α(α为锐角)后得到△AB′C′.使得B′C′交AC边于点D,点D不与点B′重合,则有下列结论:①∠ADB′=45°+α;②∠α<45°;③若AD的长为整数,则AD等于7cm;④当α=15°时,阴影部分的面积为6$\sqrt{3}$cm2.其中正确结论的序号是①②④(把所有正确的序号都填在横线上)