Question

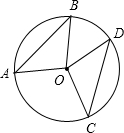
如图，若六边形ABCDEF是⊙O的内接正六边形，则∠AED=______，∠FAE=______，∠DAB=______，∠EFA=______．

Answer 1

连接OE，OB，
∵六边形ABCDEF是⊙O的内接正六边形，
∴∠EOD=∠AOB=

1

6

×360°=60°，
∵OE=OD，OA=OB，
∴△OED与△OAB是等边三角形，
∴∠ADE=∠DAB=60°；
∴∠EAD=

1

2

∠EOD=

1

2

×60°=30°，
∴∠AED=180°-∠EAD-∠ADE=90°；
∵六边形ABCDEF是正六边形，
∴∠EFA=

180°×(6-2)

6

=120°，
∵AF=EF，
∴∠FAE=

180°-120°

2

=30°．
∴∠AED=90°，∠FAE=30°，∠DAB=60°，∠EFA=120°．
故答案为：90°，30°，60°，120°．