题目内容
10.不解方程,判断所给方程:①x2+2x+3=0;②x2+4=0;③x2+x-2=0中;④2x2-px-a=0(p为常数)中,有实数根的方程有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 计算各选项中方程的根的判别式△的符号后,判断根的情况.
解答 解:①方程x2+2x+3=0的△=b2-4ac=4-12=-8<0,没有实数根;
②方程x2+4=0的△=b2-4ac=0-16=-16<0,方程没有实数根;
③x2+x-2=0的△=b2-4ac=1+8=9>0,方程有实数根;
④2x2-px-a=0(p为常数)△=b2-4ac=p2+8a(a的值不确定),方程不一定有实数根.
故选:B.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.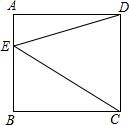 如图,在正方形ABCD中.E是AB上的三分之一点.连结DE、CE,则S△BCE:S正方形ABCD等于( )
如图,在正方形ABCD中.E是AB上的三分之一点.连结DE、CE,则S△BCE:S正方形ABCD等于( )
 如图,在正方形ABCD中.E是AB上的三分之一点.连结DE、CE,则S△BCE:S正方形ABCD等于( )
如图,在正方形ABCD中.E是AB上的三分之一点.连结DE、CE,则S△BCE:S正方形ABCD等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
19. 如图,点C把线段AB分成两条线段AC和BC,如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么下列说法错误的是( )
如图,点C把线段AB分成两条线段AC和BC,如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么下列说法错误的是( )
 如图,点C把线段AB分成两条线段AC和BC,如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么下列说法错误的是( )
如图,点C把线段AB分成两条线段AC和BC,如果$\frac{AC}{AB}$=$\frac{BC}{AC}$,那么下列说法错误的是( )| A. | 线段AB被点C黄金分割 | B. | 点C是线段AB的黄金分割点 | ||
| C. | AB与AC的比等于黄金比 | D. | AC与AB的比等于黄金比 |
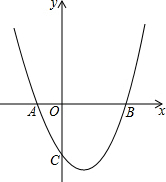 如图所示,二次函数y=x2+bx+c的图象经过点A(-1,0)和B(3,0),且与y轴交于点C.
如图所示,二次函数y=x2+bx+c的图象经过点A(-1,0)和B(3,0),且与y轴交于点C.