题目内容
已知△ABC内接于半径为1的⊙O,AB=
,AC=
,则BC边的长为 .
| 3 |
| 2 |
考点:圆周角定理,垂径定理,解直角三角形
专题:计算题
分析:如图所示,分两种情况考虑:如图1,过O作OM⊥AC,ON⊥AB,连接OA,利用垂径定理得到M、N分别为AC、AB的中点,求出AM与AN的长,利用锐角三角函数定义求出∠OAM与∠OAN的度数,进而确定出∠BAC的度数,利用余弦定理即可求出BC的长.
解答: 解:如图所示,分两种情况考虑:
解:如图所示,分两种情况考虑:
如图1,过O作OM⊥AC,ON⊥AB,连接OA,
∴M、N分别为AC、AB的中点,即AM=CM=
AC=
,AN=BN=
AB=
,
在Rt△AOM和Rt△AON中,
cos∠OAM=
=
,cos∠OAN=
=
,
∴∠OAM=45°,∠OAN=30°,
∴∠BAC=15°,
如图2所示,同理得到∠BAC=75°,
由cos15°=cos(45°-30°)=
,cos75°=
,
在△ABC中,利用余弦定理得:BC2=AC2+AB2-2AC•ABcos∠BAC=2+3-2×
×
=2-
,
或BC2=AC2+AB2-2AC•ABcos∠BAC=2+3-2×
×
=2+
,
解得:BC=
.
故答案为:
 解:如图所示,分两种情况考虑:
解:如图所示,分两种情况考虑:如图1,过O作OM⊥AC,ON⊥AB,连接OA,
∴M、N分别为AC、AB的中点,即AM=CM=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
在Rt△AOM和Rt△AON中,
cos∠OAM=
| AM |
| OA |
| ||
| 2 |
| AN |
| OA |
| ||
| 2 |
∴∠OAM=45°,∠OAN=30°,
∴∠BAC=15°,
如图2所示,同理得到∠BAC=75°,
由cos15°=cos(45°-30°)=
| ||||
| 4 |
| ||||
| 4 |
在△ABC中,利用余弦定理得:BC2=AC2+AB2-2AC•ABcos∠BAC=2+3-2×
| 6 |
| ||||
| 4 |
| 3 |
或BC2=AC2+AB2-2AC•ABcos∠BAC=2+3-2×
| 6 |
| ||||
| 4 |
| 3 |
解得:BC=
2±
|
故答案为:
2±
|
点评:此题考查了垂径定理,熟练掌握垂径定理是解本题的关键.

练习册系列答案
相关题目
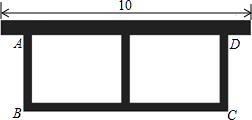 如图,园艺工人利用长24m的篱笆,一面利用墙(墙的最大长度为10m),围成中间隔有一道篱笆的长方形花圃,用以种植红玫瑰和蓝玫瑰.设花圃的边AB长为xm,BC边长为ym.
如图,园艺工人利用长24m的篱笆,一面利用墙(墙的最大长度为10m),围成中间隔有一道篱笆的长方形花圃,用以种植红玫瑰和蓝玫瑰.设花圃的边AB长为xm,BC边长为ym. 如图,点B是△ADC的边AD的延长线上一点,若∠C=50°,∠BDE=60°,∠ADC=70°.求证:DE∥AC.
如图,点B是△ADC的边AD的延长线上一点,若∠C=50°,∠BDE=60°,∠ADC=70°.求证:DE∥AC. 甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快
甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快