题目内容
设一个两位数的个位数字为a,十位数字为b (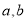
均为正整数,且
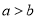),若把这个两位数的个位数字和十位数字交换位置得到一个新的两位数,则新的两位数与原两位数的差
一定是9的倍数,试说明理由.
见解析 【解析】试题分析：由题意可得出原两位数字为10b+a，新两位数字为：10a+b，然后结合整式加减法的运算法则进行求解即可． 试题解析：【解析】 原两位数字为10b+a，则新的两位数字为10a+b，则： （10a+b）﹣（10b+a）=10a+b﹣10b﹣a=9a﹣9b=9（a﹣b） ∵a和b都为正整数，且a＞b，∴a﹣b也为正整数，∴新的两位数与原两位数字的差一定...
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
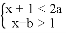的解集是2＜x＜3，则关于x的方程ax+b=0的解为_____．
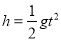表示，其中g＝10米／秒2，若物体下落的高度是180米，则下落的时间是多少秒？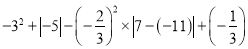
）
（
）
．
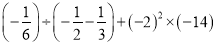
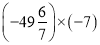
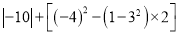
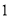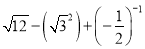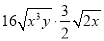