题目内容
如图,⊙O1,⊙O,⊙O2的半径均为2cm,⊙O3,⊙O4的半径均为1cm,⊙O与其他4个圆均相外切,图形既关于O1O2所在直线对称,又关于O3O4所在直线对称,则四边形O1O4O2O3的面积为( )
A.12cm2
B.24cm2
C.36cm2
D.48cm2
【答案】分析:连接O1O2,O3O4,由于图形既关于O1O2所在直线对称,又因为关于O3O4所在直线对称,故O1O2⊥O3O4,O、O1、O2共线,O、O3、O4共线,所以四边形O1O4O2O3的面积为 O1O2×O3O4.
O1O2×O3O4.
解答: 解:连接O1O2,O3O4,
解:连接O1O2,O3O4,
∵图形既关于O1O2所在直线对称,又关于O3O4所在直线对称,
∴O1O2⊥O3O4,O、O1、O2共线,O、O3、O4共线,
∵⊙O1,⊙O,⊙O2的半径均为2cm,⊙O3,⊙O4的半径均为1cm
∴⊙O的直径为4,⊙O3的直径为2,
∴O1O2=2×4=8,O3O4=4+2=6,
∴S四边形O1O4O2O3= O1O2×O3O4=
O1O2×O3O4= ×8×6=24cm2.
×8×6=24cm2.
故选B.
点评:本题考查的是相切两圆的性质,根据题意得出O1O2⊥O3O4,O、O1、O2共线,O、O3、O4共线是解答此题的关键.
 O1O2×O3O4.
O1O2×O3O4.解答:
 解:连接O1O2,O3O4,
解:连接O1O2,O3O4,∵图形既关于O1O2所在直线对称,又关于O3O4所在直线对称,
∴O1O2⊥O3O4,O、O1、O2共线,O、O3、O4共线,
∵⊙O1,⊙O,⊙O2的半径均为2cm,⊙O3,⊙O4的半径均为1cm
∴⊙O的直径为4,⊙O3的直径为2,
∴O1O2=2×4=8,O3O4=4+2=6,
∴S四边形O1O4O2O3=
 O1O2×O3O4=
O1O2×O3O4= ×8×6=24cm2.
×8×6=24cm2.故选B.
点评:本题考查的是相切两圆的性质,根据题意得出O1O2⊥O3O4,O、O1、O2共线,O、O3、O4共线是解答此题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,⊙O1与⊙O2交于点A,B,延长⊙O2的直径CA交⊙O1于点D,延长⊙O2的弦CB交⊙O1于点E.已知AC=6,AD:BC:BE=1:1:5,则DE的长是
如图,⊙O1与⊙O2交于点A,B,延长⊙O2的直径CA交⊙O1于点D,延长⊙O2的弦CB交⊙O1于点E.已知AC=6,AD:BC:BE=1:1:5,则DE的长是 ,且与直线OlO2相交于T.求AB和BT的长.
,且与直线OlO2相交于T.求AB和BT的长. 12、如图,⊙O1,⊙O2交于两点,点O1在⊙O2上,两圆的连心线交⊙O1于E,D,交⊙O2于F,交AB于点C.请你根据图中所给出的条件(不再标注其它字母,不再添加任何辅助线),写出两个线段之间的关系式:(1)
12、如图,⊙O1,⊙O2交于两点,点O1在⊙O2上,两圆的连心线交⊙O1于E,D,交⊙O2于F,交AB于点C.请你根据图中所给出的条件(不再标注其它字母,不再添加任何辅助线),写出两个线段之间的关系式:(1)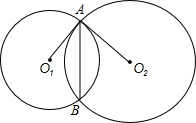 如图,⊙O1和⊙O2相交于A、B两点,且AO1、AO2分别是⊙O2、⊙O1的切线,A是切点,若⊙O1的半径r=3,⊙O2的半径R=4,求公共弦AB的长.
如图,⊙O1和⊙O2相交于A、B两点,且AO1、AO2分别是⊙O2、⊙O1的切线,A是切点,若⊙O1的半径r=3,⊙O2的半径R=4,求公共弦AB的长. 22、已知:如图,⊙O1与⊙O2相交于点A、B,过A的直线分别交两圆于点C、D,G为CD中点,BG分别交两圆于点E、F.求证:EG=FG.
22、已知:如图,⊙O1与⊙O2相交于点A、B,过A的直线分别交两圆于点C、D,G为CD中点,BG分别交两圆于点E、F.求证:EG=FG.